Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 5

По полученным значениям в выбранном масштабном коэффициенте были определены крайние (граничные)  положения выходного звена типового механизма лежащего в основе структуры сложного плоского рычажного механизма. Но, исходя из этих значений, следует, что угол рабочего хода (φ_рх) механизма, намного меньше угла холостого хода (φ_хх) механизма. Что не удовлетворяет условиям качества. Для устранения этой ошибки, необходимо поменять местами крайние (граничные) положения выходного звена механизма и поменяем направление действия силы полезного сопротивления .

Определим коэффициент неравномерности средней скорости механизма.

Коэффициент неравномерности средней скорости – это коэффициент, характеризующий отношение времени холостого хода  к времени рабочего хода:

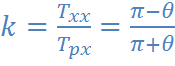                                              (1.4)

Для определения коэффициента холостого хода воспользуемся формулой (1.4), где:

T_xx – время холостого хода;

Т_рх – время рабочего хода;

Θ – угол между положениями шатуна в крайних положениях механизма;

Коэффициент неравномерности хода для группы звеньев 2 - 3:

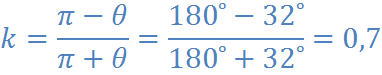
Коэффициент неравномерности хода для группы звеньев 4 - 5:

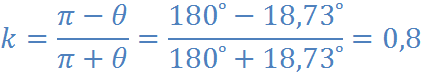
Определим ход механизма.

Ход механизма – это расстояние между начальным и конечным положениями выходного звена.

Для кривошипно-ползунного механизма ход определяется согласно:

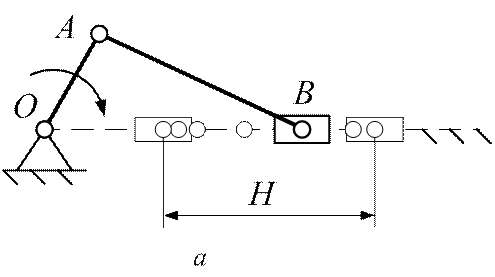
В данном случае Н=0.03 м.

7.  Кинематический анализ сложного плоского рычажного механизма.

7.1  Выбор характерных точек механизма.

Под характерными точками механизма подразумевается центры кинематических пар и центры масс звеньев. Для данного механизма используем т.O, т.A, т.B,т.О₁, т.C,т.D. Последовательно начинаем рассматривать точки с элемента стойки 0, которая взаимодействует с начальным или ведущим звеном, в данном случае кривошипом 1.

Рассмотрим точку О:

т.О относиться к шарнирно-неподвижной опоре. Траекторией движение не обладает,  поэтому скорость т.О равна 0, в любой момент времени.

Рассмотрим точку А:

т.А является центром кинематической пары 1-2, так как кривошип 1 и шатун 2 подвижные звенья, то т.А обладает траекторией движения и её скорость не равна 0. Траекторией т.А является кривая 2-го порядка, т.е окружность радиусом R₁=|OA|.

Рассмотрим точку В:

т.В является центром кинематической пары 2-3, так как шатун 2 и коромысло 3 подвижны, значит скорость т.В не равна 0. В данном случае т.В принадлежит коромыслу 3, а он в свою очередь совершает вращательное движение, значит траекторией движение будет являться кривая 2-го порядка, т.е окружность радиусом R₂=|ВО₁|.

Рассмотрим точку О₁:

т.О₁ относиться к шарнирно-неподвижной опоре. Траекторией движение не обладает,  поэтому скорость т.О₁ равна 0, в любой момент времени.

Рассмотрим точку С:

т.С является центром кинематической пары 2-4, так как шатун 2 и шатун 4 подвижны и оба совершают сложное движение, значит скорость точки т.С не равна 0. Траекторией движения т.С является кривая 2-го порядка, т.е эллипс.

Рассмотрим точку D:

т.Dявляется центром кинематической пары 4-5, так как шатун 4 и ползун 5 подвижны, значит скорость т.Dне равна 0. В данном случае т.Dпринадлежит ползуну 5, а он в свою очередь совершает поступательное движение, значит траекторией его движения будет являться прямая.

7.2  Составление векторных уравнений распределения величин скоростей между характерными точками механизма. Построение планов скоростей относительно 12(13) -ти положений кривошипа соответствующих одному циклу работы механизма.

Рассмотрим точку О и точку О₁:

Вектора скорости т.О и т.О₁ равны нулю, так как в т.Оит.О₁ находятся шарнирно-неподвижные опоры.

Рассмотрим точку А:

Вектор скорости т. A представляет собой геометрическую сумму вектора скорости т. O и скорости относительного вращательного движения т.A вокруг т. O:

_A=_O+                                                  (3.0)

Модуль скорости т.A равен:

V_A=V_AO=ω₁∙l_OA                                        (3.1)

ω₁− угловая скорость звена OA;

lOA− длина звена OA.