Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 8

 

При этом модуль вектора   найдем по выражению:

Из точки aпроводим линию параллельную шатуну АВ и откладываем на ней отрезок равный модулю вектора  и получаем точку n₁. Далее из точки n₁ строим линию перпендикулярную шатуну АВ и откладываем на ней вектор

В то же время т.B принадлежит и коромыслу 3. Коромысло 3 совершает только вращательное движение вокруг т.О₁ принадлежащей стойке и траекторией движения является кривая 2-го порядка, т. е окружность.

Следовательно вектор ускорения т. B, представляет собой геометрическую сумму вектора ускорения т. О₁, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения т. В вокруг т. О₁:

 

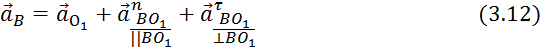
При этом модуль вектора   найдем по выражению:

Из точки О₁ проводим линию параллельную коромыслу ВO₁ и откладываем на ней отрезок равный модулю вектор а  и получаем точку n₂. Далее из точки n₂ строим линию перпендикулярную коромыслу ВO₁ и откладываем на ней вектор  На пересечении  и получаем точку b.

Рассмотрим точку С:

Вектор ускорения точки С, найдем при помощи теоремы подобия:

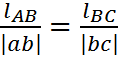                                                   (3.13)

Из формулы (3.13) выразим длину отрезка  отложим его из точки b, мы получим точку cи вектор ускорения .

Рассмотрим т. D:

Вектор ускорения т. D, принадлежит шатуну 4, представляет собой геометрическую сумму вектора ускорения т. C, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения т. Dвокруг т. C:

При этом модуль вектора   найдем по выражению:

В то же время т. Dпринадлежит ползуну 5. Ползун 5 совершает только прямолинейное возвратно-поступательное движение вдоль направляющей (прямая BO₁), следовательно, линия действия вектора ускорения т.Dпроходит параллельно прямой BO₁:

_D||BO₁

 

Из т.cпроводим линию, параллельную шатуну CD и откладываем отрезок  равный модулю вектора , получаем т. n₃. Затем через т. n₃ проводим линию перпендикулярную  шатуну DC. На пересечении перпендикуляра и направляющей ползуна (прямая BO₁), будет находиться точка d.

Определим значения ускорений характерных точек.

Замерив на плане ускорений для четвертого положения длины отрезков |ab|, |an₁|, |n₁b|, |pb|, |n₂b|, |bc|, |cn₃|, |n₃d|, |pd|, |pc|   получим:

|ab|=31,37 мм

|an₁| =  0,87 мм

|n₁b| =  31,36 мм

|pb| =  31,72 мм

|n₂b| =  24,82 мм

|pc| =  30,88 мм

|cn₃| =  6,12 мм

|n₃d| =  28,07 мм

|pd|   =  5,69 мм

|pn₂| =  19,72 мм

|bc|= 4,39 мм

|ps₁| =  0 мм

|ps₂| =  66,22 мм

|ps₃| =  31,42 мм

|ps₄| =  36,59 мм

|ps₅| =  11,38 мм

Используя найденные величины отрезков, определим модули соответствующих ускорений для четвертого положения механизма.

7.5  Определение значений и направлений действия угловых скоростей всех звеньев.

Угловое ускорение кривошипа 1 постоянно и равно 0 рад/с², т. к. угловая скорость его постоянна в любой момент времени.

Угловые ускорения шатунов 2 и 4 найдем по формуле:

ε₂=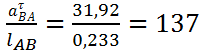 рад/c²                        (3.15)

ε₄=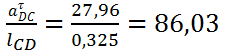рад/c²

 

Направление действия угловой скорости шатуна 2  указывает вектор ускорения , перенесенный с плана скоростей в точку В на схеме механизма. Точка А условно делается  неподвижной. При этом разрывается связь между кривошипом 1 и коромыслом 3. В этом случае точка В совместно с шатуном 2 под действием вектора получает возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки А. Полученное  направление вращательного движения шатуна 2 будет являться направлением действия угловой ускорения данного звена.