Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 7

7.3  Определение значений и направлений действия угловых скоростей всех звеньев.

Угловая скорость кривошипа 1 постоянна и равна 29,32 рад/с, т. к. скорость его постоянна в любой момент времени.

Угловые скорости шатунов 2 и 4 найдем по формуле:

ω₂=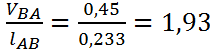 рад/c

ω₄=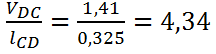рад/c

Направление действия угловой скорости шатуна 2  указывает вектор скорости , перенесенный с плана скоростей в точку В на схеме механизма. Точка А условно делается  неподвижной. При этом разрывается связь между кривошипом 1 и коромыслом 3. В этом случае точка В совместно с шатуном 2 под действием вектора   получает возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки А. Полученное  направление вращательного движения шатуна 2 будет являться направлением действия угловой скорости данного звена.

Направление действия угловой скорости шатуна 4  указывает вектор скорости , перенесенный с плана скоростей в точку Dна схеме механизма. Точка С условно делается  неподвижной. При этом разрывается связь между коромыслом 3, ползуном 5. В этом случае точка Dсовместно с шатуном 4 под действием вектора   получает, возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки С. Полученное  направление вращательного движения шатуна 4 будет являться направлением действия угловой скорости данного звена.

Угловую скорость коромысла 3 найдем по формуле:

ω₃=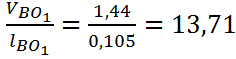 рад/c

Направление действия угловой скорости коромысла 3  указывает вектор скорости , перенесенный с плана скоростей в точку В на схеме механизма. Точка О₁ является  неподвижной. При этом разрывается связь между коромыслом 3 и шатуном 2. В этом случае точка В совместно с коромыслом 3 под действием вектора   получает возможность совершать вращательное движение в направлении действия этого вектора вокруг неподвижной точки О₁. Полученное  направление вращательного движения коромысла 3 будет являться направлением действия угловой скорости данного звена.

Ползун 5 совершает только поступательное движение, следовательно, угловая скорость этого звена равна нулю, т. е. ω₅=0 рад/с.

7.4  Составление векторных уравнений распределения величин ускорений между характерными точками механизма.

Для построения плана ускорений составим векторные уравнения.

Рассмотрим точку Oи О₁:

Так как т. О и О₁ не имеет траектории движения и =0 м/с и =0 м/с в любой момент времени, то a_O=0 м/с² и =0 м/с²

Рассмотрим точку А:

Вектор ускорения т. A представляет собой геометрическую сумму вектора ускорения т.O, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения т. A вокруг т.O:

(3.8)

В уравнении (3.8) первое слагаемое равно нулю (_O= 0), так как точка

O является неподвижной, а второе слагаемое тоже равно нулю, поскольку угловая скорость звена OA постоянна (ω₁ = const). Тогда уравнение (3.8) примет следующий вид:

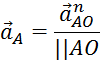
Модуль ускорения т. A  равен:

                                                 (3.9)

Подставляем полученные выражения в (3.9) получим:

(29,32)² ∙ 0,058 = 49,86 м/с²

Масштабный коэффициент плана ускорений  μ_aравен:

a_A – модуль ускорения т. А;

|pa| − произвольно выбранный отрезок, изображающий на плане ускорений вектор ускорения т. A.

Примем , тогда по выражению (3.10) получим:

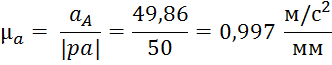
Из произвольной точки  (полюс ускорений) строим линию параллельную кривошипу АО и на нем откладываем вектор  длиной 49,86 мм, тем самым получаем точку a. Вектор  перпендикулярен кривошипу ОА и направлен в сторону его вращения. Поскольку угловая скорость звена OA постоянна (ω₁ = const), то =0 м/с².

Рассмотрим точку B:

Вектор ускорения т. B, принадлежит шатуну 2, представляет собой геометрическую сумму вектора ускорения т. А, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения т. В вокруг т. А: