Структурный анализ схем пространственного и сложного плоского рычажных механизмов, страница 3

Из анализа данных таблицы 4 следует, что исследуемый механизм состоит из семи пар пятого класса. Следовательно, р₅= 7 , а р₄=0.

Из анализа таблиц 3 и 4 следует, что данный механизм образован одной сложной замкнутой кинематической цепью (т.к звено 2 входит в состав более двух кинематических пар, т. е. содержит три вершины звена и каждое звено которой входит в состав трех кинематических пар) и содержит в своей структуре три элемент стойки, представленный звеном 0.

Полученные значения подставляем в формулу (1.2), получим:

W=3∙5-2∙7-1∙0=15-14-0=1

Результат означает, что для описания взаимного расположения звеньев данного механизма на плоскости достаточно 1 обобщенной координаты.

Анализ состава структуры сложного плоского рычажного механизма.

Для выявления структурного состава механизма разбиваем рассматриваемую схему на структурные группы Ассура и определим класс, вид, подвижность и структурную формулу.

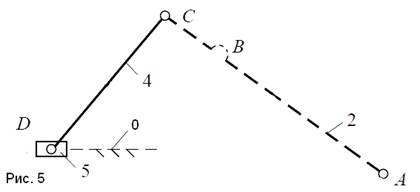Группа звеньев 4-5 (рис.5). Данная группа состоит:

из двух подвижных звеньев: шатуна 4 и ползуна 5; двух поводков: шатуна 2 и направляющей (стойки) 0; трех кинематических пар: 4-5 вращательной пары пятого класса; 2-4 вращательной пары пятого класса; 5-0 поступательной пары пятого класса. Тогда n=2 , p5=3, а p 4=0 .

Подставляя данные значения в формулу (1.2), получим:

W=3∙2-2∙3-0=0

Результат означает, что группа звеньев 4 - 5 является структурной группой.

Класс структурной группы определяется числом подвижных звеньев и числом пар, исходя из данных значений  n=2,  p₅=3, эта группа звеньев относится ко 2-му классу.

Порядок механизма определяется числом поводков, в данном случае их 2, значит, механизм обладает 2-м порядком.

Структурная формула составляется из первых букв названий кинематических пар, получаем ВВП, что соответствует 2-му виду.

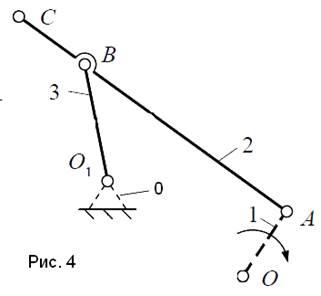Группа звеньев 2-3 (рис.4).

Данная группа состоит из двух подвижных звеньев: шатуна 2 и коромысла 3;

двух поводков: кривошипа 1 и стойки 0;

трех кинематических пар: 2-3 вращательной пары пятого класса; 1-2 вращательной пары пятого класса; 3-0 вращательной пары пятого класса. Тогда n=2,p5=3 , а p 4=0.

Подставив данные значения в формулу (1.2), получим:

W=3∙2-2∙3-0=0

Результат означает, что группа звеньев 2-3 является структурной группой.

Класс структурной группы определяется числом подвижных звеньев и числом пар, исходя из данных значений n=2, p₅=3,эта группа звеньев относится ко 2-му классу.

Порядок механизма определяется числом поводков, в данном случае их 2, значит, механизм обладает 2-м порядком.

Структурная формула составляется из первых букв названий кинематических пар, получаем ВВВ, что соответствует 1-му виду.

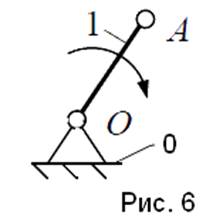
Группа звеньев 0-1 (рис.6).

Данная группа состоит из подвижного звена: кривошипа 1; шарнирно-неподвижной опоры: стойки 0; одной кинематической пары: 0-1 вращательная пара пятого класса.

Тогда n=1, p₅=1 , а p₄=0.

Подставляя данные значения в формулу (1.2), получим:

W=3∙1-2∙1-0=1

Результат означает, что для группы звеньев 0-1 существует одна обобщенная координата, следовательно, данная группа звеньев является первичным механизмом и его подвижность равна 1.

Из проведенного анализа следует, что число степеней свободы механизма равно 1; механизм имеет следующий структурный состав: первичный механизм с подвижностью равной 1 и две структурные группы 2-го класса 2-го порядка 2-го и 1-го видов.

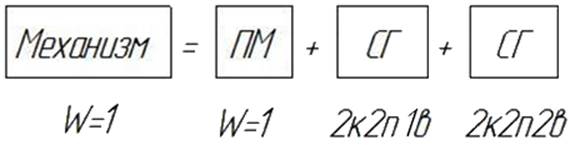
Класс и порядок механизма определяется классом и порядком наиболее сложной группы, входящей в его состав. Следовательно, данный механизм 2-го класса.

Проверка:

Для осуществления проверки сопоставим полученные значения с результатом, полученным при применении формулы Чебышева (1.2).

                                       (1.3)

 - подвижность механизма

 - подвижность первичного механизма

 - подвижность структурной группы

Полученные значения подставляя в формулу (1.3), получим:

W=1+0+0=1

Таким образом, мы получили, что результат сходиться с данными полученными при расчете по формуле (1.2), из чего следует что решение задачи выполнено правильно.