Неоднозначность – это конечная степень неопределенности, когда вся возможная информация собрана, но полностью необходимое описание не получилось.
Причины возникновения неоднозначности могут быть лингвистические и физические.
Физическая неоднозначность связана либо с наличием нескольких возможностей, каждая из которых случайным образом может стать реальностью, либо с неточностью вычислений или измерений. Таким образом, физическая неопределенность связана или с физической сущностью исследуемого явления, или с его измеряемыми проявлениями.
Лингвистическая неоднозначность связана с использованием некоторого естественного языка. Она порождается, с одной стороны, множественностью значений слов (понятий и отношений) – полисемией, с другой – неоднозначностью смысла фраз.
Математически неопределенность может быть описана стохастически, статистически, с позиций теории нечетких множеств, а также интервально.
Стохастическое описание используется тогда, когда неопределенные параметры имеют вероятностный (случайный) характер. При этом необходимо, чтобы был определен закон распределения таких случайных параметров. Стохастическим описанием занимается теория вероятностей и теория случайных процессов.
Статистическое описание является частным случаем стохастического описания. Эту форму описания применяют, когда заданы только выборочные оценки каких-либо характеристик случайной величины или наборы значений некоторых случайных параметров. Статистическим описанием занимается математическая статистика.
При описании с позиции нечетких множеств неопределенный параметр задается некоторым множеством возможных его значений, характеризующихся той или иной степенью принадлежности (с помощью так называемой функции принадлежности) объекту, описываемому этим нечетким множеством. Функция принадлежности может принимать значения от 1 (полная принадлежность) до 0 (полная непринадлежность). Интерпретацией функции принадлежности является субъективная мера того, насколько полно элемент (параметр) соответствует понятию, смысл которого описывается нечетким множеством. Этим описанием занимается теория нечетких множеств.
Интервальное описание можно использовать, когда неопределенные параметры заданы только диапазонами возможных значений (верхней и нижней границами), причем параметр может принимать любое значение внутри интервала и ему нельзя приписать никакой вероятностной меры. Интервальное описание является предметом исследования интервальной математики.
Имеется комплекс двух программ Р1, Р2. Каждая программа проходит в процессе выполнения три этапа. Управление программным комплексом осуществляется при тех же ограничениях, что и в Лабораторной работе 2. Требуется найти стратегию управления программным комплексом, обеспечивающую минимальные затраты времени на его выполнение,
1) в условиях риска задержки работы программ при выполнении последнего (третьего) этапа, если задержка во времени является случайной величиной, распределенной по показательному закону с параметрами λ1 для первой и λ2 для второй программы;
2) в условиях неопределенности, когда программный комплекс переходит из одного состояния в другое случайный образом. Предполагается, что программный комплекс может совершить любой допустимый из данного состояния переход. Вероятности переходов неизвестны.
Формализация задачи.
В условиях неопределенности требования к оптимизируемой системе и наличие модели (2.1)-(2.4), построенной в предыдущей работе, позволяют записать так называемую порождающую задачу оптимального управления программным комплексом в следующем виде:
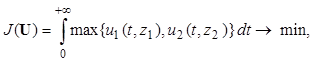 (3.1)
(3.1)
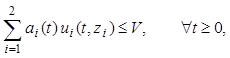 (3.2)
(3.2)
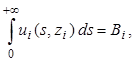 (3.3)
(3.3)
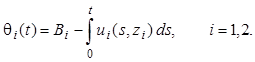 (3.4)
(3.4)
Наличие факторов неопределенности B1, B2, z1, z2.в формулах (3.1)-(3.4) не позволяет рассматривать порождающую задачу как строго сформулированную, так как неясно, что понимать под критерием и допустимым множеством задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.