|
|
2) Находим параметры предполагаемого закона распределения Количество элементов в векторе х:
Среднее значение элементов вектора х:
Дисперсия элементов вектора х:
Стандартное отклонение элементов вектора х:
Несмещенная оценка дисперсии:
Несмещенная оценка среднего квадратического отклонения
|
Границы
доверительного интервала для математического ожидания
с уровнем значимости a=0,05: ![]()
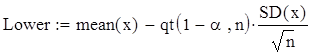
![]()
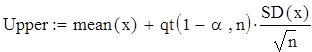
![]()
Границы доверительного интервала для среднего квадратического отклонения с уровнем значимости a=0,05:
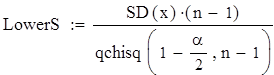
![]()
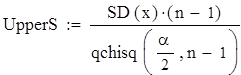
![]()
3) Разбиваем область значений х на интервалы и определяем частоты попадания в эти интервалы hk, строим гистограмму распределения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
h |
4) Определяем вероятности попадания в каждый интервал (появление значений) Рk
|
|
|
5) Вычисляем выборочное значение статистики критерия c2
c2 =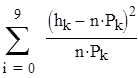
![]()
![]()
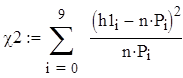
![]()
6) Принимаем статистическое решение: гипотеза не противоречит выборке на заданном уровне значимости a, если c2 < c2a-1(m-l-1)=Q, где l – число параметров распределения, которые оцениваются по выборке.
![]()
![]()
c2 < Q, следовательно гипотеза о нормальном распределении выборки х подтверждается
Граф состояний для процесса управления программным комплексом в условиях определенности
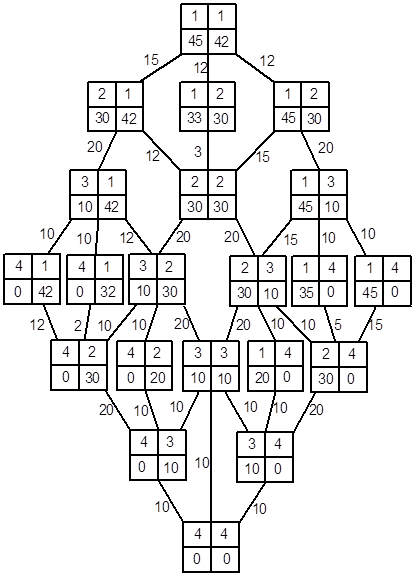
Пример выполнения расчетов в программе A_w_g |
Оглавление
|
Введение |
3 |
|
Лабораторная работа № 1 Проверка правдоподобия гипотез о законе распределения случайной величины. Критерий Пирсона . . . . . . . . . . . . . . . . . . . . . |
4 |
|
Лабораторная работа № 2 Оптимальное управление прогрммным комплексом в условиях определенности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
9 |
|
Лабораторная работа № 3 Оптимальное управление программным комплексом в условиях неопределенности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
18 |
|
Лабораторная работа № 4 Элементы теории матричных игр . . . . . . . . . . . . . . . . . . . . . . . . . |
24 |
|
Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Приложение 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Приложение 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Приложение 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Приложение 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
32 33 34 37 38 |
Учебно-методическое издание
Принятие решений в условиях неопределенности
Методические указания к лабораторным занятиям для студентов специальности «Информационные системы»
Составители: Любанова Анна Шоломовна
Даныкина Галина Борисовна
Редактор
Компьютерная верстка
Подписано в печать Формат 60´84/16.
Бумага офсетная. Печать ризографическая.
Усл.печ.л. . Уч.-изд.л. . Тираж 500 экз.
Заказ
Редакционно-издательский отдел ИЦМиЗ ФГОУ ВПО «Сибирский федеральный университет» 660025,Красноярск, ул. Вавилова, 66а
Отпечатано на участке множительной техники ИЦМиЗ ФГОУ ВПО «Сибирский федеральный университет» 660025,Красноярск, ул. Вавилова, 66а
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.