Проверка статистической гипотезы основывается на принципе, в соответствии с которым маловероятные события считаются невозможными, а события, имеющие большую вероятность (близкую к 1), считаются достоверными. Этот принцип можно реализовать следующим образом. Перед анализом выборки фиксируется некоторая малая вероятность a, называемая уровнем значимости. Пусть V - множество значений статистики Z, а Vк Í V - такое подмножество, что при условии истинности гипотезы H0 вероятность попадания статистики критерия в Vк равна a.
Обозначим через zв выборочное значение статистики Z, вычисленное по выборке наблюдений. Критерий формулируется следующим образом: отклонить гипотезу H0, если zв Î Vк; принять гипотезу H0, если zв Î V \Vк. Критерий, основанный на использовании заранее заданного уровня значимости, называют критерием значимости. Множество Vк всех значений статистики критерия Z, при которых принимается решение отклонить гипотезу H0, называется критической областью; область V \Vк называется областью принятия гипотезы H0.
Критерий c2 и его применение
Пусть х1, х2, …, хn - выборка наблюдений случайной величины Х. Проверяется гипотеза Н0, утверждающая, что Х имеет закон распределения F(x). Процедура применения критерия c2 (критерия Пирсона) для проверки гипотезы Н0 состоит из следующих этапов.
1. По выборке наблюдений случайной величины Х находятся несмещенные оценки неизвестных параметров предполагаемого закона распределения F(x).
2. Если Х - дискретная случайная величина, то определяются частоты nk, k=1, 2, …, m, с которыми каждое значение или группа значений встречается в выборке. Если Х - непрерывная случайная величина, то область ее значений разбивается на r непересекающихся интервалов D1, D2, …, Dm и определяется число элементов выборки nk, k = 1, 2, …, m, принадлежащих каждому интервалу. В обоих случаях
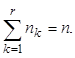
3. В случае, если Х - дискретная случайная величина, с помощью предполагаемого закона распределения F(x) вычисляются вероятности pk, k = 1, 2, …, m, с которыми случайная величина Х принимает каждое значение. В случае, когда Х - непрерывная случайная величина, следует определить вероятности pk попадания значения величины Х в каждый интервал Dk:
4. Вычисляется выборочное значение статистики критерия
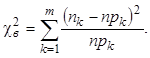(1.1)
5. Принимается статистическое решение:
гипотеза Н0 не противоречит выборке наблюдений на заданном
уровне значимости a,
если 
где l - число параметров распределения F(x), которые оцениваются по выборке; если
же 
то гипотеза Н0 отклоняется.
Постановка задачи.
Используя критерий Пирсона, при уровне значимости 0.05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности значений случайной величины X с эмпирическим распределением выборки объема n.
Методика выполнения работы в пакете MathCad
Статистическая обработка и анализ выборочной совокупности в пакете прикладных программ Mathcad (любой версии) осуществляется с помощью встроенных статистических функций Mathcad, описание которых дано в Приложении 1.
Методика выполнения работы в пакете Mathcad включает в себя первичную обработку статистических данных, построение гистограммы статистического распределения, вычисление точечных оценок (статистик) и доверительных интервалов для математического ожидания и среднего квадратического отклонения, проверку правдоподобия гипотезы о законе распределения генеральной совокупности по приведенным ниже алгоритмам. Образец документа Mathcad представлен в Приложении 2.
Первичная обработка статистических данных.
1. Выберите имя файловой переменной Mathсad и свяжите с именем файла данных соответственно варианту задания.
2. Определите диапазон числовых данных, т. е. максимальный и минимальный элементы вектора х по формулам
Mx := max(x), mx := min(x).
4. Выберите количество интервалов m (рекомендуется 10).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.