Формализация задачи и построение математической модели
Рассматриваемая ситуация относится к динамическим задачам управления ресурсами оперативной памяти в многозадачном режиме работы операционных систем. Программный комплекс представляет собой динамическую систему, состояние которой изменяется с течением времени по закону, зависящему от выбранной стратегии управления. Переход системы из одного состояния в другое осуществляется мгновенно и в любой момент времени система может находиться только в одном из своих состояний.
Для построения математической модели процесса управления данной системой прежде всего необходимо выяснить, какие параметры характеризуют ее состояние в каждый момент времени. Состояние комплекса в момент времени t определяется набором состояний {S1, …, Sn} программ Р1,…,Рn, входящих в него. В свою очередь состояние Sk программы Pk в момент t можно охарактеризовать номером этапа Nk, выполняемого программой, и временем qk(t), оставшимся до завершения работы программы (без учета времени ожидания). Таким образом, состояние комплекса в момент времени t однозначно описывается набором параметров
{(N1, q1(t)), (N2, q2(t)), …, (Nn, qn(t))}.
Управление системой заключается в распределении ресурсов оперативной памяти между программами в каждый момент времени и может быть представлено в виде вектора функций
U(t) = {u1(t), u2(t), …, un(t)}.
Если в момент
времени t
программе Pi выделен ресурс памяти aij, необходимый для выполнения j-го этапа, то ui(t) = 1. Если программе в данный момент не
выделено памяти вообще, т. е. она находится в режиме ожидания, то uj(t) = 0. Будем
считать, что в момент
завершения последнего этапа![]() программа Pi переходит в состояние «хранения на диске», не требующее
оперативной памяти, и uj(t) = 0 при
программа Pi переходит в состояние «хранения на диске», не требующее
оперативной памяти, и uj(t) = 0 при ![]() . Выбранное управление должно отвечать
условиям
. Выбранное управление должно отвечать
условиям
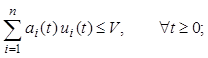 (2.1)
(2.1)
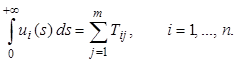 (2.2)
(2.2)
Значение функции ai(t) при каждом t равно объему оперативной памяти, предоставленной программе Pi в момент времени t.
Параметры qi(t), i = 1, …, n, связаны с ui(t) соотношениями
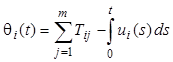
или с учетом (2.2)
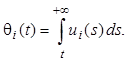 (2.3)
(2.3)
Время выполнения всего комплекса программ выражается функционалом
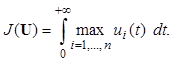 (2.4)
(2.4)
Формулы (2.1)-(2.4) описывают математическую модель рассматриваемого процесса. В рамках этой модели задача построения оптимальной стратегии управления программным комплексом заключается в отыскании вектора U(t), который удовлетворяет условиям (2.1), (2.2) и доставляет минимум фукционалу J(U).
Управление U(t) является ступенчатой векторной функцией и терпит скачок всякий раз, когда завершается выполнение очередного этапа хотя бы одной из программ Pi, i=1, …, n. Именно в такие моменты времени изменяются номера этапов Ni и происходит переход системы из одного состояния в другое в зависимости от значения управления U(t). Это обстоятельство позволяет рассматривать задачу оптимального управления программным комплексом как процесс с дискретными состояниями.
Дискретная модель для двухпрограммного комплекса
Комплекс из двух программ P1 и P2 можно рассматривать как систему, в которой протекает процесс с конечным числом дискретных состояний, каждое из которых описывается парой состояний входящих в комплекс программ: (S11, S21), (S12, S22), …, (S1k, S2k).
Рассмотрим множество этих состояний с точки зрения возможности системы переходить из состояния (S1i, S2i) в состояние (S1j, S2j) непосредственно или через другие состояния. Для этого удобно пользоваться так называемым графом состояний. Вершины графа соответствуют состояниям системы (S1i, S2i). Каждую вершину графа будем изображать прямоугольником, разделенным на четыре равные части (рис. 2.1), в которые вписаны значения четырех параметров, определяющих состояние системы: N1i и N2i - номера этапов программ P1 и P2 соответственно, q1i и q2i - рабочее время, оставшееся до завершения программ P1 и P2, без учета времени ожидания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.