Принятие решений в условиях неопределенности: Методические указания к лабораторным занятиям, страница 6

Рис. 2.1 Вершина графа состояний

Начальным состоянием системы является состояние (S₁, S₁) выполнения первого этапа обеими программами (рис. 2.2).

Рис. 2.2 Начальная вершина

В этот момент

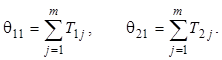
Введем для каждой из программ дополнительный  m+1-й этап «хранения на жестком диске», не требующий оперативной памяти и времени на его выполнение. Будем считать, что каждая из программ автоматически переходит в состояние «хранения на жестком диске» после завершения ее работы. Последнему (концевому) состоянию системы соответствует вершина, изображенная на рисунке 2.3.

Рис. 2.3 Концевая вершина

Стрелка (дуга), ведущая из вершины (S_1i, S_2i) в вершину (S_1j, S_2j), будет обозначать возможность перехода системы из состояния (S_1i, S_2i) в состояние (S_1j, S_2j) непосредственно, минуя другие состояния. Длина дуги равна времени этого перехода.

В условиях данной задачи из каждого состояния системы (S_1i, S_2i) (кроме концевого) теоретически можно перейти в одно из следующих состояний: 1) программа P₂ переходит к выполнению следующего этапа с номером N_2i + 1; 2) программа P₁ переходит к выполнению этапа с номером N_1i + 1; 3) одна из программ переходит к следующему этапу, а другая частично выполнила текущий этап; 4) обе программы одновременно завершают выполнение текущих этапов и переходят к следующим.

Первое состояние означает, что программа P₁ находится в режиме ожидания. Время перехода в этом случае равно времени выполнения текущего этапа программой P₂. Соответственно, система оказывается во втором состоянии, если программа P₂ находится в режиме ожидания. Время перехода в это состояние совпадает со временем выполнения текущего этапа программы P₁.

Переход к третьему или четвертому состоянию возможен, когда программы выполняются одновременно. Время перехода в этом случае равно минимальному времени необходимому для завершения своего этапа хотя бы одной из программ.

Таким образом в каждом состоянии возможны три стратегии управления системой: а) программе P₁ выделяется ресурс памяти для выполнения очередного этапа, программа P₂ ожидает своей очереди; б) программа P₁ находится в режиме ожидания, программа P₂ выполняется; в) обе программы выполняются одновременно.

Решение о допустимости переходов из одних состояний в другие принимается на основании ограничений задачи. В рамках рассматриваемой задачи переход из состояния (S_1i, S_2i) в состояние (S_1j, S_2j) считается допустимым, если соблюдены три условия. Во-первых, необходимый для перехода ресурс оперативной памяти не превышает V мбайт. Далее, согласно приоритету ресурсы памяти выделяются в первую очередь той программе, которая уже приступила к фактическому выполнению очередного этапа, но не успела его завершить. Наконец, ни одна из программ не может вернуться к уже завершенным этапам или пропустить еще невыполненный этап. Так что при допустимом переходе номер этапа хотя бы одной из программ должен увеличиться ровно на 1.

Таким образом, граф состояний задает бинарное отношение R_S на множестве всех состояний системы: состояние (S_1i, S_2i) находится в отношении R_S с состоянием (S_1j, S_2j) тогда и только тогда, когда допустим переход из (S_1i, S_2i) в (S_1j, S_2j). Геометрическое построение графа удобнее всего начинать с первой вершины (источника) и вести последовательно, выявляя все допустимые стратегии управления в каждой из вершин. Это позволит определить очередные состояния, в которые система может перейти в результате применения той или иной допустимой стратегии.

Пример графа состояний для процесса управления комплексом из двух программ представлен в Приложении 3. Граф построен при следующих исходных данных: V = 64 мбайт, T₁₁ = 15, T₁₂ = 20, T₁₃ = 10, T₂₁ = 12, T₂₂ = 20, T₂₃ = 10, a₁₁ = 30, a₁₂ = 45, a₁₃ = 20, a₂₁ = 25, a₂₂ = 40, a₂₃ = 15.

Задача принятия решений.