Для выхода из этой ситуации необходимо построить математическую модель рассматриваемой задачи, исключающую факторы неопределенности. При таком подходе в процессе принятия решения неопределенная ситуация тем или иным способом преобразуется в детерминированную, при которой можно однозначно выбрать окончательное решение.
В условиях риска задержки выполнения программ параметры zi являются случайными величинами, соответствующими времени задержки. В свою очередь
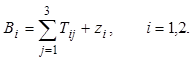
Так же как в предыдущей работе комплекс двух программ P1 и P2 можно рассматривать как систему, в которой протекает процесс с конечным числом дискретных состояний, и строить дискретную модель управления этой системой. Поскольку время выполнения третьего этапа каждой из программ случайно, процедура принятия решения сводится к отысканию кратчайших путей на графе состояний в условиях стохастической неопределенности. Наиболее часто для исключения такой неопределенности используют M-модель стохастического программирования, которая позволяет найти решение, наилучшее в среднем.
По условию задачи задержка zi подчиняется показательному закону распределения с плотностью вероятности
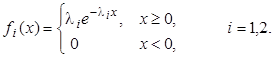
Следовательно,
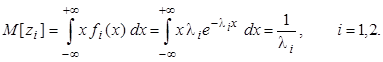
Так что время выполнения третьего этапа программой Pi в среднем равно Ti3 + M[zi]. Теперь время выполнения каждой из программ становится неслучайным, и задача сводится к детерминированной модели, изученной в предыдущей лабораторной работе. Методика построения графа состояний остается той же, что и в условиях определенности. Кратчайшие пути на графе задают стратегии управления комплексом, наилучшие в среднем.
Если случайными являются сами переходы программного комплекса из одного состояния в другое, а не время, и вероятности переходов неизвестны, то следует пользоваться принципом недостаточного обоснования. Согласно этому принципу все допустимые переходы из текущего состояния считаются равновероятными. Это значит, что если в текущем состоянии допустимы все три стратегии управления системой, то вероятность применения каждой из них равна 1/3. В случае двух допустимых стратегий вероятность равна 1/2. Таким образом, принцип недостаточного обоснования позволяет свести данную ситуацию к задаче (3.1)-(3.4), в которой случайные параметры zi =Z, i=1,2, где Z - номер пути на графе состояний. Вероятность выбора системой каждого из путей (стратегий управления) равна произведению вероятностей всех переходов или дуг, составляющих путь. Величины Bi не случайны и
![]()
![]()
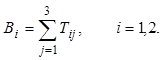
Поскольку каждый допустимый вектор управления U(t, Z) = (u1(t, Z), u2(t, Z)) однозначно задается номером пути Z, длину пути J(U) можно рассматривать как неслучайную функцию, которая каждому значению k случайного номера пути Z ставит в соответствие значение длины этого пути
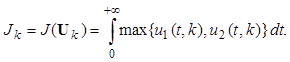
Фактически значение Jk равно сумме длин дуг на графе состояний, составляющих путь с номером k.
Несмотря на то, что ситуация формально сведена к задаче стохастического программирования, необходимо учитывать первоначальный характер неопределенности при выборе модели критерия (целевой функции). В данном случае наиболее приемлемым представляется использование критерия предельного уровня [4], согласно которому оптимальная стратегия содержится среди путей, удовлетворяющих условию
![]() (3.5)
(3.5)
как наиболее вероятных. Математическое ожидание M[J(U)] и дисперсия D[J(U)] функции J(U) находятся по формулам [5]
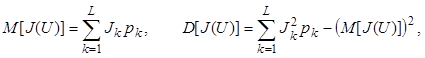
где L - число всех путей на графе состояний, pk - вероятность выбора системой пути с номером k.
В Приложении 4 представлены расчеты вероятностей переходов системы из одного состояния в другое, выполненные для графа из Приложения 2 с помощью программы A_w_G.
1. Получить задание у преподавателя.
2. Найти ожидаемое время выполнения третьего этапа каждой из программ, рассчитав математическое ожидание задержки, и построить граф состояний.
3. Определить наилучшую в среднем стратегию управления комплексом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.