Принятие решений в условиях неопределенности: Методические указания к лабораторным занятиям, страница 12

Число b_j - максимальный возможный проигрыш игрока B, если он пользуется стратегией B_j (j = 1, …, n):

Число

называют нижней ценой игры (максимином), а соответствующую ему чистую стратегию - максиминной. Число

называют верхней ценой игры (минимаксом), а соответствующую чистую стратегию - минимаксной. Максимин не превосходит минимакса, то есть a £ b.

Если a = b, то говорят, что игра имеет седловую точку в чистых стратегиях и чистую цену игры v = a = b. Пару чистых стратегий A_i* и B_j*, соответствующих a и b, называют седловой точкой матричной игры, а элемент a_i*j* платежной матрицы, стоящий на пересечении i*-й строки и j*-го столбца - седловым элементом платежной матрицы. Стратегии A_i* и B_j*, образующие седловую точку, являются оптимальными. Тройку { A_i*; B_j*; v} называют решением игры.

Для игр без седловых точек оптимальные стратегии игроков находятся в области смешанных стратегий. Смешанной стратегией игрока A называют вектор p = (p₁, …, p_m), компоненты которого удовлетворяют условиям

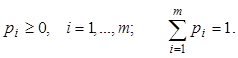
Смешанной стратегией игрока B называют вектор q = (q₁, …, q_n), где

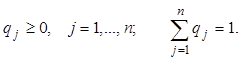
Здесь p_i и q_j - вероятности, с которыми игроки A и B выбирают свои чистые стратегии A_i и B_j. При использовании смешанных стратегий игра приобретает случайный характер, случайной становится и величина выигрыша игрока A (проигрыша игрока B). Эта величина является функцией смешанных стратегий p и q и определяется по формуле

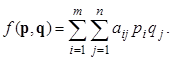
Функцию f(p, q) называют платежной или функцией выигрыша.

Смешанные стратегии p* и q* называются оптимальными, если они образуют седловую точку для платежной функции f(p, q), то есть

Величину f(p*, q*) = v называют ценой игры.

Статистические игры

Статистические игры образуют специальный класс матричных игр, в которых одним из участников является человек или группа людей, объединенных общностью цели (игрок  A - статистик), а другим - «природа» (игрок П). Под термином «природа» подразумевается весь комплекс внешних условий, при которых статистику приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи статистика. Статистик располагает m стратегиями A₁, …, A_m, природа может реализовать любое из n различных состояний П₁, …, П_n. Действуя против природы, статистик  пользуется как чистыми A_i, так и смешанными p = (p₁, …, p_m) стратегиями. Если статистик имеет возможность численно оценить (величиной a_ij) последствия применения каждой своей чистой стратегии A_i при любом состоянии П_j природы, то игру можно задать платежной матрицей.

При выборе оптимальной стратегии статистика пользуются различными критериями. Если вероятности q_j состояний П_j природы известны, то пользуются критериями Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимает чистая стратегия A_i, при которой максимизируется средний выигрыш статистика, то есть обеспечивается

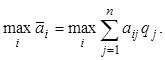
Если статистику представляются в равной мере правдоподобными все состояния П_j природы, то q₁ = … = q_n = 1/n и оптимальной по критерию Лапласа считается стратегия A_i, обеспечивающая

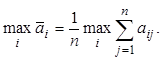
При неизвестных вероятностях состояний природы пользуются критериями Вальда, Сэвиджа, Гурвица. Оптимальной по критерию Вальда (максиминному критерию) считается чистая стратегия A_i, при которой статистику обеспечивается

Для смешанных стратегий критерий Вальда формулируется так: оптимальной считается смешанная стратегияp*, найденная из условия

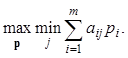
Оптимальной по критерию Сэвиджа считается та чистая стратегия A_i, при которой минимизируется величина максимального риска r_ij, то есть обеспечивается

Для смешанных стратегий согласно критерию Сэвиджа оптимальной считается стратегияp*, найденная из условия

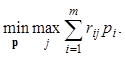
Оптимальной по критерию Гурвица считается чистая стратегия A_i, при выборе которой достигается

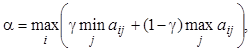
где g принадлежит интервалу (0, 1) и выбирается из субъективных соображений.

Анализ практических ситуаций проводится по нескольким критериям одновременно, что позволяет глубже исследовать суть явления и выбрать наиболее обоснованное решение.