Принятие решений в условиях неопределенности: Методические указания к лабораторным занятиям, страница 3

5.   Задайте диапазон изменения номера узла (конца интервала) с использованием дискретного аргумента k.

6.   Используя дискретный аргумент k как нижний индекс, определите элементы вектора узлов с помощью формулы

int_k := mx+ k/m*(Mx- mx).

Построение гистограммы

1.  Используя встроенную функцию hist, вычислите вектор частот, с которыми элементы выборки, содержащиеся в векторе х, попадают в интервалы, представляемые вектором  int. Для этого определите функцию

h := hist(int,x)

2.  Выберите в панели инструментов Графика кнопку построения гистограмм. В пустом поле появившейся на экране рамки напечатайте h (имя вектора частот). Затем щелкните левой кнопкой мыши в любом месте вне рамки.

3.  Отрегулируйте положение гистограммы по своему усмотрению. Для этого вызовите окно управления двойным щелчком левой кнопки мыши на гистограмме.

Точечные оценки (статистики) и доверительные интервалы

1.  Вычислите статистики, т. е. выборочное среднее, выборочную дисперсию и среднее квадратическое отклонение статистической выборки x с помощью соответствующих встроенных функций mean(x), var(x), stdev(x).

2.  Стандартные функции var и stdev вычисляют смещенные оценки дисперсии и среднего квадратического отклонения. Предпочтительнее использовать несмещенные оценки. Задайте количество элементов n в выборке х и определите несмещенные оценки дисперсии и среднего квадратического отклонения, напечатав

n := length(x),

,        .

3.  Найдите границы доверительного интервала для математического ожидания с уровнем значимости a = 0.05 при неизвестной дисперсии по следующим формулам:

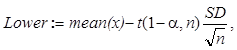
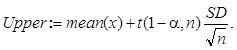
Значение квантиля распределения Стьюдента t(1-a, n) находится с помощью встроенной функции qt с параметрами p = 1 - a и d = n.

4.  Найдите границы доверительного интервала для среднего квадратического отклонения с уровнем значимости a = 0.05 по следующим формулам:

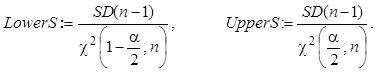
Значения квантиля c²-распределения c²(a/2, n) и c²(1-a/2, n) находятся с помощью встроенной функции qchisq.

Проверка правдоподобия гипотезы о законе распределения генеральной совокупности

1.  Найдите вероятности p_i попадания значений генеральной совокупности в каждый интервал int_i, напечатав (см. приложение 2)

a := mean(x)

p₀ := pnorm(int₀, a, SD)

i := 1.. m-1

p_i := pnorm(int_i+1, a, SD) - pnorm(int_i, a, SD)

p_m := 1 - pnorm(int_m, a, SD)

2.  Найдите критическое значение c_крит с помощью встроенной  функции qchisq с параметрами p = 1 - a и d = m - l -1, где l - число параметров распределения. Для нормального закона l = 2.

3.  Вычислите выборочное значение статистики критерия  по формуле (1.1). Сравните полученное значение с c_крит и примите статистическое решение.

Порядок выполнения работы

1.  Получить задание у преподавателя (файл данных).

2.  Провести первичную обработку выборки (построить интервальное распределение), построить гистограмму интервального распределения, вычислить несмещенные точечные оценки параметров распределения и найти границы доверительных интервалов.

3.  С помощью критерия c² проверить правдоподобие гипотезы о том, что генеральная совокупность имеет нормальный закон распределения с параметрами, равными полученным несмещенным статистическим оценкам математического ожидания и среднего квадратического отклонения.

4.  Оформить отчет, включив в него титульный лист, краткое описание необходимых теоретических сведений, распечатку файла данных, распечатку документа Mathcad (образец см. в приложении 2).

Контрольные вопросы и задания

1.  Что такое статистическая гипотеза?

2.  Какая гипотеза называется простой?

3.  Какая гипотеза называется сложной?

4.  Дайте определение критерия проверки гипотез.

5.  Какой критерий называют критерием значимости?

6.  Что такое критическая область и область принятия решений?

7.  Какая гипотеза проверяется в данной лабораторной работе?

8.  Приведите формулу, по которой вычисляется выборочное значение статистики критерия c² для проверки гипотезы Н₀.