Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 9

                                            (114)

следовательно,  Подставив в полученное выражение данные задачи, получим:  с.

Электрическая емкость контура  выражается из равенства  для собственной частоты колебаний в контуре:

,                                         (115)

где при переходе к правой части использовано соотношение (114).

Подставив в зависимость энергии электрического поля от времени (см. равенство (51))

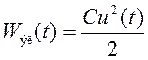                                                  (116)

выражение (115) и закон колебаний напряжения, заданный в условии, получим:

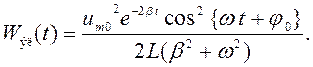                                (117)

Так как , , а , в момент времени  энергия электрического поля

 

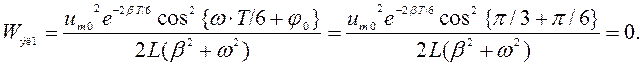
Ответ: , с;

 .

7. ВЫНУЖДЕННЫЕ  МЕХАНИЧЕСКИЕ  КОЛЕБАНИЯ[6]

7.1. Основные формулы и обозначения

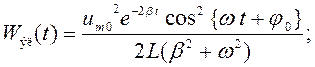
Гармоническая вынуждающая сила задается выражением:  в котором  и  – амплитуда и  циклическая частота колебаний этой силы соответственно.

Закон вынужденных гармонических колебаний при установившемся движении имеет вид:

                                      (118)

где

 –                                (119)

амплитуда;

 – разность фаз между колебанием и вынуждающей силой (),

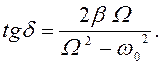                                                (120)

Резонансная частота

                                               (121)

резонансная амплитуда

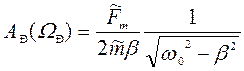.                                     (122)

7.2. Примеры решения задач

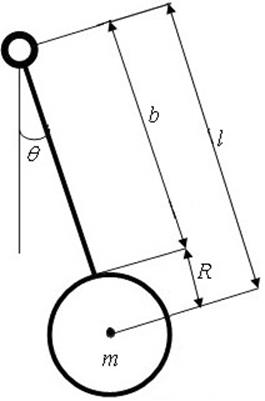
З а д а ч а  16. Шар массой 17,1 т и радиусом 80 см, служащий для слома домов, подвешен на тросе длиной 3,6 м. Верхний конец троса закреплен, масса троса пренебрежимо мала по сравнению с массой шара. Шар раскачивают в вертикальной плоскости, приложив вынуждающую силу, момент которой относительно оси вращения меняется по закону:  По какому закону будет изменяться угол отклонения троса от положения равновесия, если частота и амплитуда момента вынуждающей силы соответственно равны  с^-1 и         200 кН·м? Коэффициент затухания равен 5,4 с^-1. Найти полную энергию колебаний системы.

Дано:  кг;  м;  м;  с-1;  Н·м;  с-1;  м/с2. Найти:

Решение. По условию задачи массой троса можно пренебречь, а шар – считать физическим маятником, ось колебаний которого находится на расстоянии                                        (123) от центра шара, поэтому обобщенной координатой удобно выбрать угол отклонения троса от равновесного (вертикального) положения[7]   (рис. 9) и записать закон установившихся вынужденных колебаний шара (118) для этого угла:                                 (124)

где, с учетом того, что обобщенной вынуждающей силой является момент силы  а обобщенной массой – момент инерции шара относительно оси колебаний , выражение (119) для амплитуды имеет вид:

            (125)

Разность фаз  между углом и вынуждающей силой вычисляется по формуле (120):

                  .          (126)

Момент инерции шара относительно оси колебаний определяется с помощью теоремы Гюйгенса – Штейнера (см. сноску на стр. 7) с учетом формулы (123):                                                                                                Рис. 9

.             (127)

Собственная частота колебаний шара как физического маятника

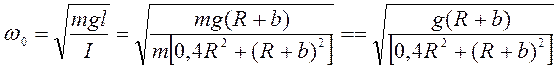.          (128)

Подставляя равенства (127) и (128) в формулы (125) и (126), получим расчетные выражения для параметров вынужденных колебаний:

                                   

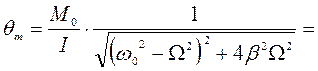
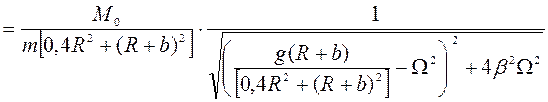;           (129)

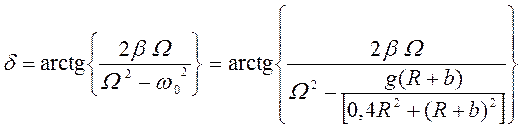,    (130)

Подставляем в соотношения (129) и (130) данные задачи:

                                

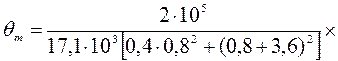
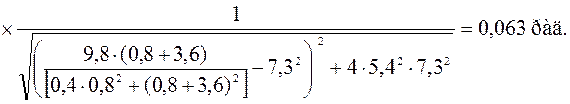        (131)

°.

Таким образом, все параметры, определяющие закон (124), найдены.

Полная энергия колебаний маятника вычисляется с учетом численного значения амплитуды (131) по формуле: 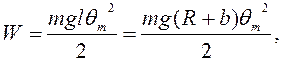  Дж.

Ответ:  где  рад;  с^-1; °;

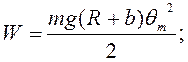
  Дж.

З а д а ч а  17. При какой частоте колебаний гармонической вынуждающей силы амплитуда колебаний груза массой 420 г на пружинке жесткостью 20 Н/м принимает максимальное значение? Найти это значение, если амплитуда колебаний силы равна 8,5 Н, а коэффициент затухания колебаний грузика   равен 4,3 с^-1.

Дано:  кг;  Н/м;  Н;  с-1. Найти:

Решение. Собственная частота колебаний груза .                                                 (132) Максимальное значение амплитуды вынужденных колебаний  наблюдается при резонансе и определяется по формуле (122). Резонансная частота определяется по формуле (121).