Выразив в формуле (64)
собственную частоту колебаний через период ![]() получим:
получим:
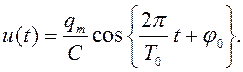 (65)
(65)
Подставив в формулу (65)
численные данные при ![]() найдем:
найдем:  В.
В.
Ответ: 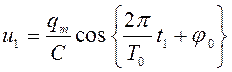 ,
, ![]() В.
В.
З а д а ч а 9. В идеальном колебательном контуре с индуктивностью 100 мГн совершаются гармонические колебания с частотой 400 Гц. Найти емкость конденсатора и закон изменения силы тока в контуре, если в начальный момент времени сила тока была максимальной и равной 16 мА.
|
Дано:
Найти: |
Решение. Закон колебаний силы тока в идеальном колебательном контуре имеет вид:
где
|
собственная частота;
![]() –
начальная фаза колебаний, которая определяется из закона (66) при
–
начальная фаза колебаний, которая определяется из закона (66) при ![]() с в соответствии с начальным условием
с в соответствии с начальным условием ![]() :
:
![]() (68)
(68)
Подставив выражения (67) и (68) в закон (66), получим зависимость силы тока в рассматриваемом контуре от времени:
![]() . (69)
. (69)
Емкость конденсатора
найдем из выражения ![]() полученного подстановкой в
соотношение (67) формулы
полученного подстановкой в
соотношение (67) формулы ![]() для собственной частоты
колебаний в контуре:
для собственной частоты
колебаний в контуре: ![]() Отсюда
Отсюда ![]() Ф.
Ф.
Ответ: ![]() мА;
мА;
![]()
![]() мкФ.
мкФ.
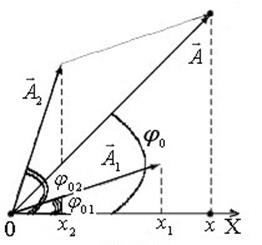 При сложении
гармонических колебаний одного направления и одинаковой частоты, например, колебаний
При сложении
гармонических колебаний одного направления и одинаковой частоты, например, колебаний ![]() и
и ![]() удобно
использовать метод векторных диаграмм. Каждое колебание изображается вектором
на плоскости (например,
удобно
использовать метод векторных диаграмм. Каждое колебание изображается вектором
на плоскости (например, ![]() и
и ![]() ). Длина этого вектора равна амплитуде
соответствующего колебания. Угол между вектором и Рис. 5 горизонтальной
осью равен фазе соответствующего колебания в данный момент времени. Вектор
). Длина этого вектора равна амплитуде
соответствующего колебания. Угол между вектором и Рис. 5 горизонтальной
осью равен фазе соответствующего колебания в данный момент времени. Вектор ![]() описывающий результирующее колебание, строится
по правилам сложения векторов. Частота результирующего колебания
описывающий результирующее колебание, строится
по правилам сложения векторов. Частота результирующего колебания ![]() также равна
также равна ![]() Амплитуда
и начальная фаза результирующего колебания определяются по диаграмме для
начального момента времени (рис. 5) и вычисляются соответственно по формулам:
Амплитуда
и начальная фаза результирующего колебания определяются по диаграмме для
начального момента времени (рис. 5) и вычисляются соответственно по формулам:
![]() (70)
(70)
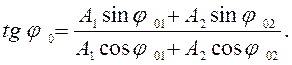 (71)
(71)
При сложении гармонических
взаимно перпендикулярных колебаний, совершаемых точкой в плоскости ![]() ,
например, колебаний
,
например, колебаний
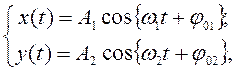 (72)
(72)
уравнение траектории движения содержит
только переменные ![]() и
и ![]() но не содержит
времени
но не содержит
времени ![]() Следовательно, уравнение траектории можно
найти, если каким-либо образом исключить из формул (72) время, например,
выразить
Следовательно, уравнение траектории можно
найти, если каким-либо образом исключить из формул (72) время, например,
выразить ![]() через
через ![]() или
или ![]() .
.
Если при этом отношение частот
(периодов) ![]() является рациональной дробью (отношением
целых чисел), то траектория оказывается замкнутой, а движение – периодическим.
является рациональной дробью (отношением
целых чисел), то траектория оказывается замкнутой, а движение – периодическим.
З а д а ч а 10. Построить
векторную диаграмму в начальный момент времени при сложении двух гармонических
колебаний одинаковой частоты и одного направления. Найти графически и
аналитически амплитуду и начальную фазу результирующего колебания. Записать
закон результирующего колебания. Законы складываемых колебаний имеют вид: ![]()
![]() где
где ![]() см;
см; ![]() см;
см; ![]() с-1;
с-1; ![]()
![]()
|
Дано:
Найти: |
Решение. Чтобы найти амплитуду и
начальную фазу результирующего колебания, можно воспользоваться формулами (70),
(71), предварительно заменив по формуле приведения |
где
![]() . (74)
. (74)
Тогда
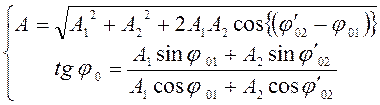 . (75)
. (75)
Подставляя в равенства (75)
численные данные и учитывая формулу (74), получим: ![]() см;
см; 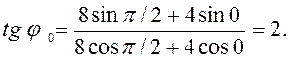 Отсюда
Отсюда ![]() °
°![]() рад. Следовательно, закон результирующего
колебания имеет вид:
рад. Следовательно, закон результирующего
колебания имеет вид: ![]() где
где ![]() см;
см; ![]() с-1;
с-1; ![]() рад.
рад.
Начертим векторную
диаграмму сложения колебаний в начальный момент времени (рис. 6). Для этого в
соответствии с правилами построения, изложенными в подразделе 4.1, сопоставим колебанию
![]() вектор
вектор ![]() длиной
длиной ![]() , который направим под углом
, который направим под углом ![]() к горизонтальной оси
к горизонтальной оси ![]() , т. е. вертикально вверх; колебанию
, т. е. вертикально вверх; колебанию ![]() сопоставим вектор
сопоставим вектор ![]() длиной
длиной
![]() , который направим под углом
, который направим под углом ![]() к горизонтальной оси
к горизонтальной оси ![]() , т. е. отложим его в направлении оси (см. рис.
6). Результирующее колебание будет описываться вектором
, т. е. отложим его в направлении оси (см. рис.
6). Результирующее колебание будет описываться вектором ![]() длиной
длиной
![]() полученным по правилу параллелограмма
сложением векторов
полученным по правилу параллелограмма
сложением векторов ![]() и
и ![]() Угол,
образованный вектором
Угол,
образованный вектором ![]() и осью
и осью ![]() равен
начальной фазе результирующего колебания
равен
начальной фазе результирующего колебания ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.