Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 2

,                                                          (1)

где  – обобщенная координата;

 – циклическая частота колебаний;

 – обобщенное ускорение.

Циклическая частота связана с частотой  соотношением: . Период колебаний  .

Обобщенная возвращающая сила, действующая на линейный гармонический осциллятор и приводящая к ускорению: , подчиняется (как и сила упругости, возникающая при малых деформациях тел) закону Гука:

,                                                     (2)

где

 –                                                     (3)

обобщенный коэффициент жесткости;

– обобщенная масса.

Собственная частота колебаний определяется по формулам:

1)  – для пружинного маятника с массой  и коэффициентом упругости пружины  

2)  – математического маятника с длиной нити

3)  – физического маятника с массой  моментом инерции  и расстоянием от центра инерции до оси вращения  ( – ускорение свободного падения).

1.2. Примеры решения задач

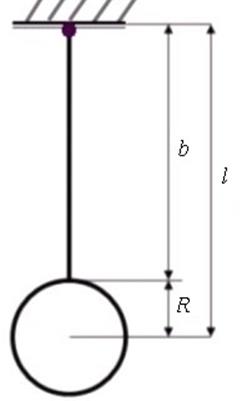
З а д а ч а  1. Маятник настенных часов можно представить в виде невесомого стержня длиной 30 см, к концу которого припаян диск радиусом 8 см и массой 2,5 кг (рис. 1). Маятник колеблется в вертикальной плоскости вокруг горизонтальной оси, проходящей через верхний конец стержня. Диск расположен в плоскости колебаний. Найти период малых свободных незатухающих колебаний маятника.

  – момент инерции маятника,

 –                                                    (5)

расстояние от центра инерции до оси вращения;  – ускорение свободного падения.

Период связан с циклической частотой соотношением:

.                                      (6)

Подставив в соотношение (6) формулу (4), получим:

.                                 (7)

Стержень невесом, поэтому масса и момент инерции маятника равны соответственно массе и              Рис. 1                  моменту инерции диска, который вычисляется с использованием теоремы Гюйгенса – Штейнера[2], так как ось колебаний не проходит через центр инерции диска:

,        (8)

где  – момент инерции диска относительно оси, перпендикулярной диску и проходящей через его центр.

С учетом равенств (5) и (8) выражение (7) принимает вид:

.       (9)

Подставляем данные задачи:

с.            

Ответ: ,  с.

З а д а ч а  2. Маленькая заряженная дробинка может без трения двигаться внутри вертикально расположенной трубки, прикрепленной нижним концом к заряженному шару (рис. 2). Заряды шара и дробинки одноименные. Когда дробинка находится в состоянии равновесия, расстояние от нее до центра шара – 80 см. Найти собственную частоту малых вертикальных колебаний дробинки.

Обобщенный коэффициент жесткости системы определяется в соответствии с законом Гука как коэффициент пропорциональности между возвращающей силой и обобщенной координатой:

                                                    (11)

Обобщенная масса системы определяется как коэффициент пропорциональности между возвращающей силой и обобщенным ускорением:

                                                   (12)

Таким образом, основная цель при решении данной задачи – найти эти обобщенные параметры, используя явный вид возвращающей силы, действующей на выведенный из положения равновесия шарик. Для этого сначала рассмотрим и найдем силы, действующие на дробинку, находящуюся в состоянии равновесия. Результирующая этих сил равна нулю:  так как при равновесии механической системы все действующие на нее силы скомпенсированы. Затем найдем результирующую силу  действующую на дробинку, находящуюся в неравновесном состоянии в положении с координатой  Эта сила и будет возвращающей: