С учетом соотношения (132) выражения (121) и (122) принимают вид:
![]() (133)
(133)
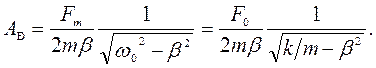 (134)
(134)
Подставив в выражения (129)
и (130) данные задачи, получим: ![]() с-1;
с-1; 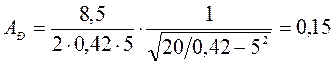 м.
м.
Ответ: ![]()
![]()
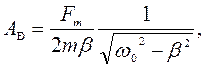
![]() м.
м.
 Гармоническая
вынуждающая электродвижущая сила задается выражением:
Гармоническая
вынуждающая электродвижущая сила задается выражением: ![]() ,
в котором
,
в котором ![]() и
и ![]() – амплитуда
и циклическая частота колебаний электродвижущей силы соответственно. Закон
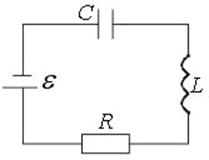
установившихся вынужденных гармонических колебаний в контуре (рис. 10)
выражается формулой:
– амплитуда
и циклическая частота колебаний электродвижущей силы соответственно. Закон
установившихся вынужденных гармонических колебаний в контуре (рис. 10)
выражается формулой: ![]() где амплитуда
где амплитуда 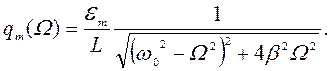 Разность фаз
Разность фаз ![]() опреде-
опреде-
Рис. 10 ляется по формуле (120).
Сила тока в цепи ![]() . Амплитуда силы тока
. Амплитуда силы тока ![]() где
где ![]() – модуль
импеданса (комплексного сопротивления) контура;
– модуль
импеданса (комплексного сопротивления) контура; ![]() и
и ![]() – емкостное и индуктивное реактивные сопротивления
соответственно.
– емкостное и индуктивное реактивные сопротивления
соответственно.
При частоте ![]() в цепи наблюдается резонанс тока. При этом
модуль импеданса равен активному сопротивлению:
в цепи наблюдается резонанс тока. При этом
модуль импеданса равен активному сопротивлению: ![]()
З а д а ч а 18. К
источнику переменного напряжения, меняющегося по закону ![]() где
где
![]() В,
В, ![]() с-1,
последовательно подключены конденсатор емкостью 120 мкФ, катушка индуктивностью
0,34 мГн и резистор сопротивлением 180 Ом (см. рис. 10). Найти законы изменения
заряда и силы тока в цепи.
с-1,
последовательно подключены конденсатор емкостью 120 мкФ, катушка индуктивностью
0,34 мГн и резистор сопротивлением 180 Ом (см. рис. 10). Найти законы изменения
заряда и силы тока в цепи.
|
Дано:
Найти: |
Решение. Законы установившихся вынужденных колебаний заряда и силы тока в цепи имеют вид:
Амплитуда колебаний силы тока
|
где ![]() – модуль
импеданса.
– модуль
импеданса.
Разность фаз ![]() колебаний заряда и вынуждающей электродвижущей
силы вычисляется по формуле:
колебаний заряда и вынуждающей электродвижущей
силы вычисляется по формуле:
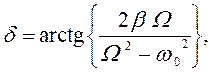
![]() (138)
(138)
где
![]() – (139)
– (139)
собственная частота колебаний в контуре;
![]() – (140)
– (140)
коэффициент затухания.
Комбинируя выражения (137) – (140), получим:
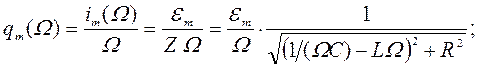 (141)
(141)
 (142)
(142)
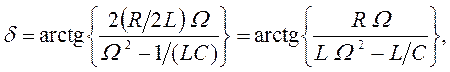
![]() (143)
(143)
Подставляем в выражения (141) – (143)
численные данные: 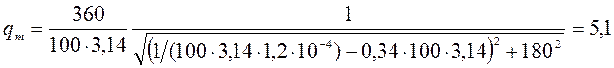 мКл;
мКл;
 А;
А;
 °.
°.
Ответ: ![]() где
где ![]() мКл,
мКл, ![]() °;
°;
![]() где
где ![]() А,
А, ![]() °.
°.
З а д а ч а 19. Найти добротность колебательного контура, если резонанс напряжения на обкладках конденсатора, входящего в контур, наблюдается при частоте, в 1,0008 раза меньшей частоты затухающих колебаний в этом контуре.
|
Дано:
Найти: |
Решение. Напряжение на обкладках
конденсатора |
Резонансная частота вынужденных колебаний определяется по формуле (121):
![]() (144)
(144)
где ![]() – собственная
частота колебаний в контуре;
– собственная
частота колебаний в контуре;
![]() –
коэффициент затухания.
–
коэффициент затухания.
Соотношение для частоты затухающих колебаний имеет вид:
![]() (145)
(145)
Выражения (144) и (145)
позволяют найти отношение ![]() . Если
. Если ![]() , то затухание можно считать малым. Тогда
для определения добротности можно применить формулу:
, то затухание можно считать малым. Тогда
для определения добротности можно применить формулу:
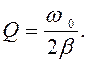 (146)
(146)
Возведем соотношения (144)
и (145) в квадрат: ![]() ;
; ![]() .
Отсюда
.
Отсюда
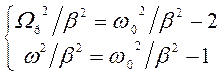 . (147)
. (147)
С учетом отношения левых частей равенств (147)
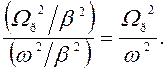 (148)
(148)
отношение правых частей равенств (147)
принимает вид: 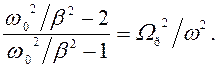 Отсюда
Отсюда
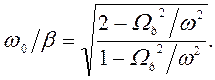 (149)
(149)
Подставляя в выражение (149) численные данные, получим:

Следовательно, ![]() , поэтому формула (146) применима. Подставляя
в формулу (146) соотношение (149), получим:
, поэтому формула (146) применима. Подставляя
в формулу (146) соотношение (149), получим:
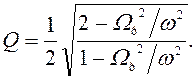 (150)
(150)
Используем численные данные:
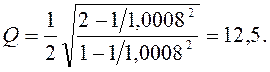
Ответ: 
![]()
УПРУГИЕ И ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Пусть плоская
монохроматическая (гармоническая) волна с длиной ![]() и периодом
и периодом
![]() распространяется в направлении оси
распространяется в направлении оси ![]() с (фазовой) скоростью
с (фазовой) скоростью ![]() Тогда уравнение, описывающее колебания
точек такой волны (уравнение бегущей волны), имеет вид:
Тогда уравнение, описывающее колебания
точек такой волны (уравнение бегущей волны), имеет вид:
![]() (151)
(151)
где ![]() – смещение
колеблющейся точки волны от положения равновесия;
– смещение
колеблющейся точки волны от положения равновесия;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.