Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 7

Ответ: где см; с^-1; Рис. 6 рад.

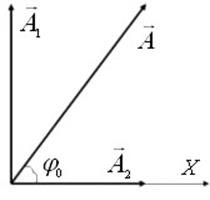
З а д а ч а 11. Получить уравнение траектории частицы и построить траекторию в плоскости , если частица одновременно участвует в двух взаимно перпендикулярных колебаниях: где см, см.

Дано:

Найти:

Решение.

Чтобы найти уравнение траектории точки на плоскости необходимо из системы уравнений

; (76)

(77)

исключить время. Для этого из уравнения (76) выразим :

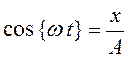. (78)

Отсюда

. (79)

Преобразовав и возведя в квадрат уравнение (77), а затем, последовательно применив формулы приведения и двойного аргумента к тригонометрическим функциям, получим:

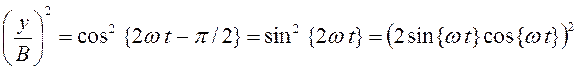. (80)

Используя соотношения (78) и (79), из выражения (80) можно исключить время и получить уравнение траектории:

(81)

Для построения траектории в плоскости выберем наиболее удобные точки. Это точки, имеющие равную нулю, наибольшую и наименьшую из возможных ординату () или абсциссу ().

Таблица 2

Используя уравнение траектории (81), найдем вторые координаты этих точек Рис. 7

(см. Табл. 2).

Траектория, построенная по этим точкам, показана на рис. 7. Координата достигает максимума по модулю четырежды, а – дважды. Это объясняется соответствующим отношением частот: за время одного колебания вдоль оси точка совершает два колебания вдоль оси

Ответ:

5. СВОБОДНЫЕ ЗАТУХАЮЩИЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

5.1. Основные формулы и обозначения

На систему, совершающую свободные затухающие колебания, действуют две обобщенных силы: возвращающая сила, задаваемая формулой (2), и сила сопротивления:

(82)

где – обобщенный коэффициент сопротивления среды.

Закон затухающих колебаний имеет вид:

(83)

где – экспоненциально убывающая амплитуда;

– начальная амплитуда, вещественная константа;

– коэффициент затухания,

– (условная) циклическая частота затухающих колебаний [1, 4, 6, 7].

Потенциальная и кинетическая энергия затухающих колебаний определяются формулами (23), в которые подставляются выражения для расчета скорости и смещения при затухающих колебаниях.

В случае малого затухания поэтому при усреднении за период пренебрегают изменением множителя :

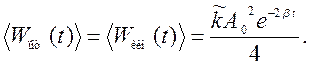
Средняя за период полная энергия затухающих колебаний

(84)

где 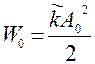– начальное значение энергии.

Логарифмический декремент затухания

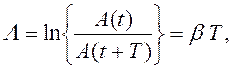(85)

где – (условный) период затухающих колебаний [1, 4, 6, 7].

Добротность колебательной системы

(86)

при малом затухании вычисляется по формуле:

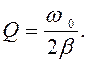(87)

Добротность также принято выражать через отношение запасенной в системе энергии (84) к средней за период потере энергии

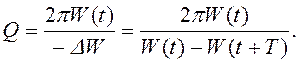(88)

5.2. Примеры решения задач

З а д а ч а 12. Гиря массой 680 г подвешена на пружине жесткостью 16,3 Н/м. За 24 полных колебания их амплитуда уменьшилась в 1,44 раза. Определить коэффициент затухания, циклическую частоту затухающих колебаний и добротность маятника.

Дано:

кг;