|
Дано:
Найти: |
Решение. Длина волны связана с частотой и скоростью распространения соотношением:
Скорость распространения
электромагнитной волны в вакууме –
поэтому вычисляемые по формуле (162) длины волны в вакууме и в среде соответственно равны:
|
Подставив в соотношения
(164) численные данные, получим: 
м; 
м.
Напряженность
электрического поля 
(см. рис. 11), где
. (165)
Амплитуду колебаний
напряженности электрического поля найдем, пользуясь соотношением 
:
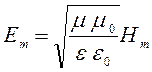. (166)
Циклическую частоту и волновое число найдем, пользуясь соответствующими определениями и формулой (163):
; (167)
. (168)
С учетом выражений (166) – (168) формула (165) принимает вид:
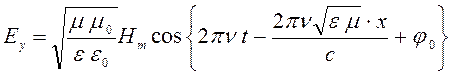. (169)
Подставив в соотношение
(169) численные данные, получим при 
(с учетом равенства 
) и 
:
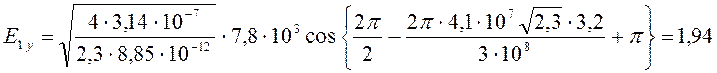МВ/м.
Ответ: 
, 
м;
, 
м;
МВ/м.
1. С а в е л ь е в И. В. Курс общей физики: В 5 кн. Кн. 1. Механика / И. В. С а в е л ь е в. М.: Наука, 1998. 336 с.; М.: АСТ, 2004. 336 с.
2. С а в е л ь е в И. В. Курс общей физики: В 5 кн. Кн. 2. Электричество и магнетизм / И. В. С а в е л ь е в. М.: Наука, 1998. 336 с.; М.: АСТ, 2005. 336 с.
3. С а в е л ь е в И. В. Курс общей физики: В 5 кн. Кн. 4. Волны. Оптика / И. В. С а в е л ь е в. М.: Наука, 1998. 256 с.; М.: АСТ, 2004. 256 с.
4. Д ж а н к о л и Д. Физика / Д. Д ж а н к о л и. М.: Мир, Т.1. 1989. 667 с.
5. Д ж а н к о л и Д. Физика / Д. Д ж а н к о л и. М.: Мир, Т.2. 1989. 667 с.
6. Т р о ф и м о в а Т. И. Курс физики / Т. И. Т р о ф и м о в а. М.: Высшая школа, 2004. 542 с.; М.: Академия, 2006. 560 с.
7. Физический энциклопедический словарь / Под ред. А.М. Прохорова. М.: Советская энциклопедия, 1983. 928 с.
8. С е р д ю к О. И. Колебания и волны. Задачи: Методические указания к решению задач по физике / О. И. С е р д ю к, Г. Б. Т о д е р / Омский гос. ун-т путей сообщения. Омск, 2011. 40 с.
9. Ч е р т о в А. Г. Задачник по физике / А. Г. Ч е р т о в, А. А. В о р о б ь е в. М.: Интеграл-Пресс, 1997. 544 с.; М.: Физматлит, 2009. 640 с.
Учебное издание
СЕРДЮК Ольга Ивановна, ТОДЕР Георгий Борисович
КОЛЕБАНИЯ И ВОЛНЫ:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Редактор Н. А. Майорова
Корректор Д. А. Волнина
***
Подписано в печать . .2011. Формат 60 ´ 84 1/16.
Плоская печать. Бумага офсетная. Усл. печ. л. . Уч.-изд. л. .
Тираж 1000 экз. Заказ .
**
Редакционно-издательский отдел ОмГУПСа
Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
О. И. СЕРДЮК, Г. Б. ТОДЕР
КОЛЕБАНИЯ И ВОЛНЫ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ОМСК 2011
[1] Здесь и ниже точка над любой величиной означает производную этой величины по времени.
[2] Если ось не проходит через центр масс, то момент инерции тела относительно этой оси определяется по теореме Гюйгенса – Штейнера: , где IC – момент инерции тела относительно оси , параллельной оси и проходящей через его центр масс; l – расстояние между осями и .
[3] Общая формула разложения выражения при в ряд с точностью до членов первого порядка малости имеет вид: .
[4] Графики функций и имеют одинаковую форму, но сдвинуты друг относительно друга на угол , поэтому с помощью преобразований и всегда можно перейти от одной функции к другой.
[5] Здесь предполагается, что в положении равновесия () потенциальная энергия равна нулю.
[6] В разделе 7 рассматриваются только установившиеся колебания, происходящие под действием гармонической вынуждающей силы.
[7] В этом случае: 1) обобщенными силами являются моменты сил, обобщенной массой маятника – момент инерции, обобщенными скоростью и ускорением – угловые скорость и ускорение 2) формулы для кинетической, потенциальной и полной энергии колебаний соответственно имеют вид: ; ; .
[8] В разделе 8 рассматриваются только установившиеся вынужденные колебания, происходящие при наличии в контуре источника переменной электродвижущей силы, меняющейся со временем по гармоническому закону.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
; 
;
Гц;
А/м;
;
Ф/м;
Гн/м;
м/с;
м; 
.
; 
; 
.
. (162)
, в среде – 
, (163)