Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 3

(13)

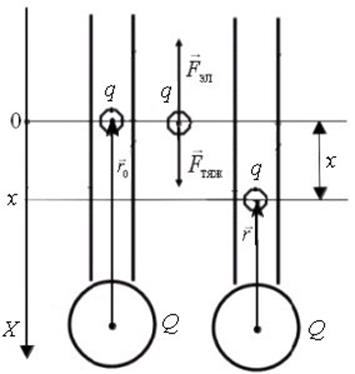
Считая дробинку материальной точкой, направим ось абсцисс вертикально, например, вниз, а в качестве начала координат выберем положение равновесия дробинки. Тогда координата дробинки Рис. 2 характеризует ее смещение от положения равновесия, т. е. является обобщенной координатой.

В равновесии на дробинку действуют две силы: сила тяжести направленная вертикально вниз, и направленная в противоположную сторону сила электрического отталкивания где и – заряды дробинки и шара соответственно, вектор проведен из центра шара к дробинке (в состоянии равновесия). Согласно принципу суперпозиции сил 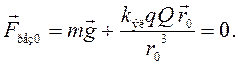Следовательно, модули силы тяжести и силы электрического отталкивания равны:

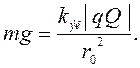(14)

На выведенную из равновесия дробинку действуют те же две силы. Сила тяжести не меняется, а сила электрического отталкивания 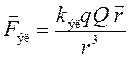изменяется: она уменьшается по модулю в случае удаления дробинки от шара и увеличивается в случае ее приближения к шару. Вектор проведен из центра шара к дробинке, причем Согласно принципу суперпозиции сил результирующая сила Проекция на ось рассчитывается по формуле:

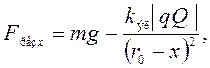(15)

где при смещении дробинки вниз и при ее смещении вверх.

При малых колебаниях , поэтому выражение можно разложить в ряд по степеням , ограничившись линейным приближением, т. е., оставив только два первых слагаемых ряда и пренебрегая остальными слагаемыми в силу их малости относительно двух первых[3]:

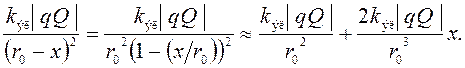(16)

Подставив разложение (16) в формулу (15), получим:

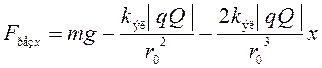. (17)

Объединяя равенства (14), (15) и (17), получим в явном виде выражение для расчета возвращающей силы:

. (18)

Сравнивая формулы (18) и (11), найдем

(19)

С учетом уравнения (14) выражение (19) упрощается и принимает вид:

(20)

С другой стороны, сравнив основное уравнение динамики материальной точки для дробинки записанное с учетом равенства (13), с выражением (12), заметим, что . Используя равенство и выражение (20) для подстановки в формулу (10), получим окончательное выражение для собственной частоты: Подставляем в полученное выражение данные задачи: с^-1.

Ответ: , с^-1.

2. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

2.1. Основные формулы и обозначения

Закон гармонических колебаний является решением уравнения (1) и имеет вид[4]:

(21)

или

(22)

где – колеблющаяся величина (обобщенная координата),

– время;

– амплитуда (обозначается также );

– фаза;

– начальная фаза;

– циклическая частота колебаний.

Проекции скорости 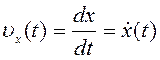и ускорения 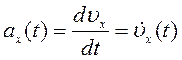на ось меняются также по гармоническому закону.

Потенциальная[5] и кинетическая энергия механических колебаний вычисляются по формулам:

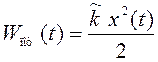; (23)

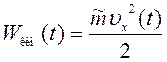. (24)

Полная энергия колебаний не зависит от времени:

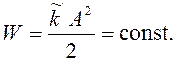(25)

2.2. Примеры решения задач

З а д а ч а 3. Частица массой 14 г совершает свободные незатухающие колебания по закону синуса с периодом 3,7 с и с начальной фазой, равной нулю. Полная энергия колеблющейся частицы – 0,016 мДж. Найдите наибольшее значение модуля возвращающей силы, действующей на частицу.

Дано:

кг;