Физика \ Физика

Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 5

Знак в правой части формулы (48) определяется выбором направления оси вдоль которой происходят колебания маятника. Если, например, направить ось в сторону смещения груза сразу после удара, то сразу после начала колебаний координата груза будет положительной, т. е. зависимость (48) примет вид:

(49)

где м; с.

Скорость колебаний можно найти как производную по времени от координаты, которая задана функцией (49):

(50)

Ответ: где м, с;

где м/с.

3. СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ИДЕАЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

3.1. Основные формулы и обозначения

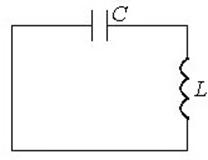
Собственная частота колебаний заряда , силы тока и напряжения в идеальном колебательном контуре (рис. 3) определяется выражением: где – индуктивность; – ёмкость контура. Заряд совершает гармонические колебания: – амплитуда колебаний заряда. Сила тока и напряжение связаны с зарядом соотношениями: и Энергия электрического и магнитного полей вычисляется по формулам:

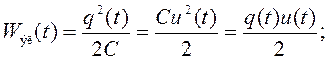(51)

Рис. 3 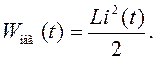(52)

3.2. Примеры решения задач

З а д а ч а 7. Идеальный колебательный контур состоит из конденсатора емкостью 200 мкФ и катушки индуктивностью 3 мГн. Конденсатор зарядили количеством электричества 70 мкКл и замкнули на катушку. Найти зависимости от времени энергии электрического и магнитного полей и построить графики этих зависимостей в пределах половины периода колебаний заряда.

Дано:

Ф;

мГн;

Кл.

Найти и построить графики: и

Решение.

Энергия электрического и магнитного полей определяется по формулам:

(53)

(54)

где – заряд на пластинах конденсатора;

– сила тока, протекающего через катушку.

Так как контур идеальный, заряд совершает гармонические колебания:

(55) где

– (56)

собственная частота колебаний в контуре;

– начальная фаза, определяемая из закона (51) при с: , откуда

(57)

Согласно условию задачи в момент начала колебаний заряженный конденсатор замкнули на катушку, поэтому заряд на пластинах не может быть больше начального. Таким образом, амплитуда колебаний заряда равна начальному заряду:

(58)

Подставив начальное условие (58) в формулу (57), получим:

(59)

Таким образом, законы (55) и (53) колебаний заряда и энергии электрического поля в контуре с учетом равенства (56) принимают вид:

(60)

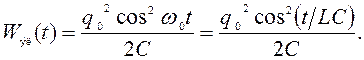(61)

Закон колебаний силы тока найдем, взяв производную по времени от правой части формулы (60):

(62) поэтому зависимость энергии магнитного поля от времени (50) с учетом равенства (56) принимает вид:

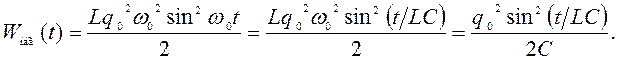(63)

Таблица 1
	мкДж	мкДж
	мкДж	мкДж
	мкДж	мкДж

Через полную энергию мкДж и период колебаний мс зависимости энергии от времени (61) и (63) представляются в виде: ; . Удобство этих формул заключается в значительном облегчении построения графиков и вычисления энергии при выборе значений времени , отвечающих экстремумам гармонических функций. Построим графики. Значения энергии в выбранные моменты времени в пределах половины периода колебаний заряда показаны в табл. 1. Графики зависимости энергии от времени изображены на рис. 4.

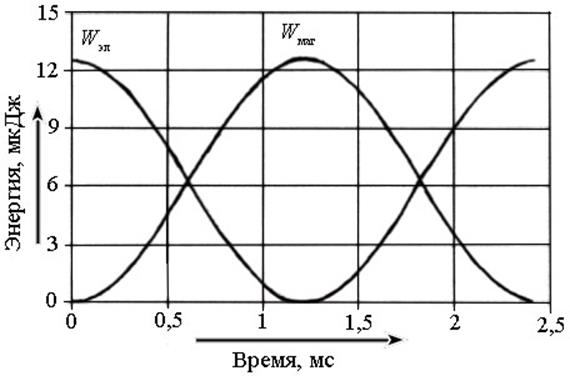
Рис. 4

Ответ: , , где мкДж;

мс.

З а д а ч а 8. В идеальном колебательном контуре с емкостью 6 мкФ заряд на обкладках конденсатора меняется по закону: где мкКл; Найти разность потенциалов (напряжение) на обкладках конденсатора спустя четверть периода колебаний.