Физика \ Физика

Колебания и волны. Примеры решения задач: Методические указания к решению задач по физике, страница 8

Соотношения (91), (92), (94) представляют собой систему трех уравнений с тремя неизвестными: , , Возводя обе части выражения (94) в квадрат, а затем, подставляя в полученное равенство формулы (92) и (91), получим:

(95)

Отсюда, учитывая равенство (93), выразим :

(96)

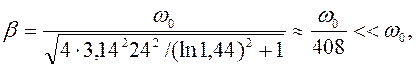(97)

следовательно, выполнено условие малости затухания и добротность системы можно найти по формуле (87) с учетом выражения (96):

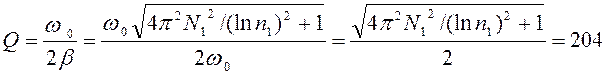. (98)

Подстановка значения (93) в формулы (91) и (97) позволяет с учетом малости найти соответственно численные значения и : с^-1; с^-1.

Ответ: с^-1;

с^-1;

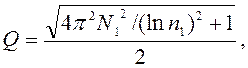
З а д а ч а 13. Энергия затухающих колебаний осциллятора, происходящих в вязкой среде с малым затуханием, за 5 мин уменьшилась в 37 раз. Определить коэффициент сопротивления среды, если масса осциллятора равна 120 г.

Дано:

с;

кг.

Найти:

Решение.

Коэффициент сопротивления среды связан с коэффициентом затухания колебаний и массой осциллятора:

(99)

Для определения воспользуемся выражением (84) для средней за период полной энергии затухающих колебаний:

(100)

Отсюда для интересующего момента времени получим: и выразим :

(101)

Объединив формулы (95) и (96), получим:

. (102)

Подстановка численных данных в выражение (102) приводит к следующему результату: .

Ответ: , .

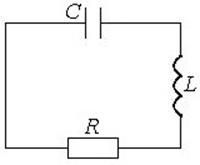6. СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В РЕАЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ

6.1. Основные формулы и обозначения

В реальном колебательном контуре (рис. 8) колебания заряда являются затухающими: , где – частота свободных затухающих колебаний; – коэффициент затухания. Средняя за период полная энергия, логарифмический декремент затухания, добротность вычисляются по формулам (84) – (88). Рис. 8

6.2. Примеры решения задач

14. Колебательный контур состоит из конденсатора емкостью 0,8 мкФ, катушки индуктивностью 1,25 мГн и сопротивления. Найти: 1) сопротивление контура, при котором за 14 мс амплитуда колебаний заряда на обкладках конденсатора уменьшается в 1,7 раза; 2) логарифмический декремент затухания.

Дано:

Ф;

Гн.

с;

Найти: ; .

Решение.

Сопротивление связано с коэффициентом затухания колебаний и индуктивностью контура:

(103)

Для определения воспользуемся выражением

(104)

для расчета амплитуды затухающих колебаний.

Отсюда для интересующего момента времени получим: и выразим :

(105)

Объединив формулы (105) и (103), получим:

(106)

Подстановка численных данных приводит к следующему результату: .

Логарифмический декремент затухания

(107)

где – период затухающих колебаний, связанный с их циклической частотой

(108)

соотношением:

; (109)

– (110)

собственная частота колебаний в контуре.

Для того, чтобы найти приравняем друг другу квадраты периода и полученные из формул (107) и (109):

(111)

а затем в выражение (111) подставим формулы для частот (108) и (110): . Отсюда, учитывая равенство (105), выразим :

(112)

Подставив в формулу (112) данные задачи, получим: .

Ответ: , ;

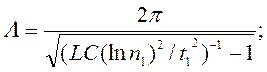
З а д а ч а 15. В реальном колебательном контуре напряжение на обкладках конденсатора меняется по закону: где В; с^-1; с^-1; . Найти: 1) период собственных колебаний в контуре, если его индуктивность равна 0,85 Гн; 2) энергию электрического поля спустя время, равное 1/6 периода от начала затухающих колебаний.