Амплитуда колебаний может быть найдена, исходя из выражения (25) для полной энергии:
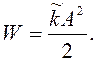(31)
по формуле:
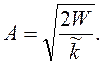(32)
Объединив соотношение (3) и формулу (27), получим выражение для расчета обобщенного коэффициента жесткости:
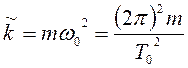. (33)
Подставив равенства (30)
и (32), а затем – (33) в выражение (29), получим максимальное значение модуля
возвращающей силы (другими словами, амплитуду колебаний силы): 
Отсюда после подстановки данных получим: 
.
Ответ: 
, 
.
З а д а ч а 4. Математический маятник массой 250 г и длиной 1,2 м совершает гармонические колебания с амплитудой 72 мм. Определить: 1) полную энергию колебаний; 2) модуль скорости колебаний в момент времени, когда смещение маятника от положения равновесия равно 36 мм.
|
Дано:
Найти: |
Решение. 1) Полную энергию колебаний маятника вычислим по формуле (25):
|
, (35)
а затем – выражение
(36)
для собственной частоты колебаний математического маятника:
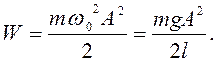(37)
Подставив в формулу (37)
численные данные, получим: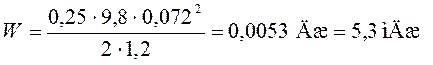 
.
2) Колебания гармонические, поэтому выполняется закон сохранения энергии:
(38)
Полная энергия определяется выражением (37), а потенциальная и кинетическая – формулами (23), (24), следовательно, с учетом равенств (35) и (36)
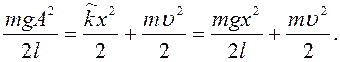(39)
Отсюда в момент времени 
. (40)
Подставив в формулу (40)
численные значения всех величин, получим: 
м/с.
Ответ: 
мДж;
, 
м/с.
З а д а ч а 5. Материальная
точка совершает свободные гармонические колебания вдоль оси 
так, что проекция ее скорости на ось меняется с течением времени по закону: 
, где 
м/с, 
рад/с, 
. Найти
момент времени, ближайший к началу колебаний, когда проекция ускорения на ось
колебаний равна 
м/с2.
|
Дано:
Найти: |
Решение. Ускорение можно найти как производную по времени от скорости:
Выразим фазу колебаний из
соотношения (41): |
(42)
где 
–
целое.
Подстановка численных
данных в правую часть формулы (42) приводит к ряду значений времени: 
распадающемуся на две последовательности,
соответствующие двум значениям – 
и 
– функции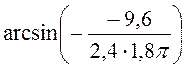 
:
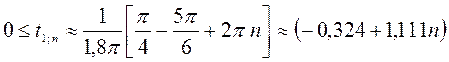с; (43)
с. (44)
Выбираем из всех
возможных решений, представленных последовательностями (43) и (44), минимальное
(ближайшее к нулю) положительное значение времени: 
с,
которое получается при подстановке значения 
в ряд (43).
Ответ: с.
З а д а ч а 6. Горизонтальный пружинный маятник массой 170 г выводят из положения равновесия горизонтальным ударом по грузу, после которого маятник начинает совершать гармонические колебания с амплитудой 2 см. Записать закон колебаний и зависимость скорости колебаний от времени, если коэффициент упругости пружины равен 80 Н/м.
|
Дано:
Найти: |
Решение. Так как маятник совершает гармонические колебания, зависимость его смещения от положения равновесия от времени в общем случае имеет вид:
|
с – (46)
собственная частота колебаний маятника.
Чтобы записать закон (45)
для рассматриваемого в задаче пружинного маятника в явном виде, необходимо
найти начальную фазу колебаний. Для этого подставим в закон начальное условие: 
(начальное условие 
м
означает, что в момент начала колебаний 
с
маятник находился в положении равновесия), откуда
(47)
Подставив соотношение (45) и значение начальной фазы (47) в закон (45), получим зависимость:
(48)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
м;
кг;
м;
м.
; 
, (34) подставив в нее соотношение (3) для
обобщенного коэффициента жесткости 
м/с2.
(41)
, найдем время: 
кг;
м;
Н/м;
; 
.
(45) где 
–
начальная фаза;