Восстановление изношенных деталей машин. Разработка технологии восстановления распределительного вала, страница 20

Привод перемещения в полношаговом режиме требует 6625 импульсов на один метр, в полушаговом – 13250. Соответственно, скорость перемещения каретки может быть программно задана  любой  в целое число раз меньшей 151 мм/сек. Максимальная реализуемая скорость перемещения детали зависит от суммарного веса детали и каретки. Это ограничение не приводит к затруднениям при выборе режимов напыления, так как крупные детали требуют меньших скоростей перемещения.

Стабильность скоростей вращения и перемещения обеспечивается применением шаговых двигателей и компьютерным управлением, плавность хода – применением резиновых ремней.

Напряжение, подаваемое на шаговые двигатели, не превышает 24 в, а драйверы снабжены защитой от перегрузок и короткого замыкания.

Ток через фазы включенного шагового двигателя протекает всегда, независимо от того, вращается ротор или нет. Рассеиваемая в обмотках двигателя мощность составляет 16 Вт, а рабочая температура корпуса двигателя – 40-50°С.

Вал шагового двигателя конический, шпонка отсутствует. Сцепление вала с муфтой осуществляется за счет трения, поэтому втулка муфты «сажается» на вал по горяче-прессовой посадке с нагревом муфты до 100-150 градусов. Самораспрессовка муфты является наиболее вероятной причиной отказа привода. Вал двигателя тонкий, поэтому при монтаже привода следует избегать приложения ощутимых усилий.

3.4 Конструкторские расчеты пружины

Применяя метод сечений, нетрудно заметить, что в сечении проволоки возникают небольшие по величине изгибающий момент и продольная сила, а также поперечная сила Q=F и крутящий момент T_k=FD/2.По величине касательные напряжения сдвига обычно составляют 2…5% от напряжения кручения, а остальные виды деформации учитываются в поправочном коэффициенте.

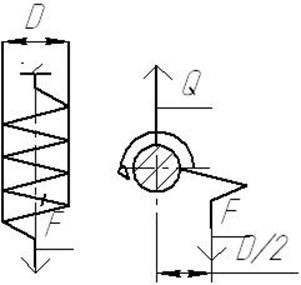
Рисунок 3.1 – Схема пружины

Введем следующие обозначения:                          

D – средний диаметр витка пружины;

d – диаметр сечения проволоки пружины;

C=D/d – индекс пружины, принимаем C=9:

n – общее количество витков пружины;

m – число рабочих витков, в данном случае m = n так как пружина       работает на растяжение.

Условие прочности пружины с учетом поправочного коэффициента будет иметь вид по формуле [23]

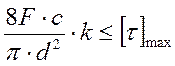,                                         (3.4.1)

Где F – продольная сила, Н;

- максимально допустимое значение напряжений в пружине, Н;

Значение поправочного коэффициента определяется по эмпирической формуле [23]

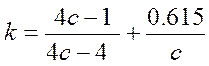                                       (3.4.2)

Где c – индекс пружины, с=9;

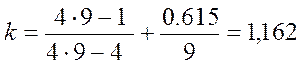
Продольная сила будет складываться F=W+F_дгн;

Где W - Сопротивление передвижению тележки, Н [24]

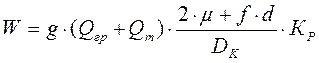,                           (3.4.3)

где g – ускорение свободного падения, g = 9,81 м/с ²;

Q_гр – грузоподъемность, Q_гр = 12кг;

Q_т – масса тележки, Q_т = 80 кг;

μ – коэффициент трения качения колеса, μ = 0,3…1 мм;

f– коэффициент трения в опоре, f= 0,01…0,02, для подшипников скольжения;

d – посадочный диаметр колеса, d = 20 мм;

D_К– диаметр колеса, D_К = 80 мм;

К_Р – коэффициент сопротивления от трения реборд колеса и торцов втулок, К_Р = 1,4…3,0.

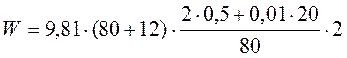 = 27,1 Н;

 – сила с которой действует заряд при напылении;

                                                                (3.4.4)

где m– масса заряда, m=1г;

a– ускорение заряда, a=600…1000 м/с²

;

Тогда продольная сила  F будет равна:

F=27,1+1=28,1 Н;

Из формулы (3.4.1) находим диаметр сечения проволоки пружины:

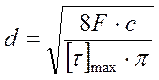,                                            (3.4.5)

где F – продольная сила, F=28,1 Н;

- максимально допустимое значение напряжений в пружине,=45 Н;

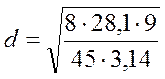=4,63 мм;

По справочнику выбираем стандартную пружину d=4,75 мм;

Тогда диаметр пружины будет равен:

 , где d – диаметр проволоки пружины, d=4,75 мм;

c – индекс пружины, c=9;

 мм;

Сила при максимальной деформации F_max :

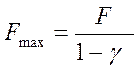 , где F – продольная сила, F=28,1 Н;

γ – относительный инерционный зазор, принимается из справочника γ=0,16

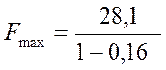 =33,5 Н;

Жесткость пружины С, Н/м;

 ,

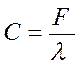Где F  – продольная сила, F=28,1Н;

λ – деформация пружины, λ =10·10^{-3 м;}

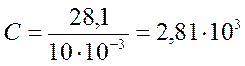 Н/м;

Максимальная деформация λ_max м;

 ;

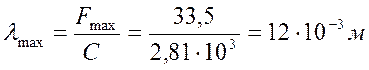Расчетное касательное напряжение τ, Н;