Ответы на экзаменационные вопросы № 1-55 по дисциплине "Экономический анализ" (Предмет экономического анализа. Классификация видов анализа), страница 5

Факторы, которые рассматривались ранее, фиксированы на отчетном уровне – все, что стоит слева.

Факторы, которые не рассматривали – на уровне базиса – все, что стоит справа.

 

При методе цепных подстановок число расчетных или условно-расчетных значений результативного показателя равно числу факторов минус 1.

 Проверка обязательна:

Прием абс. разниц

y=a*b*c

1.  ∆y(a)=(a1-a0)*b0*c0

2.  ∆y(b)=a1*(b1-b0)*c0

3.  ∆y(c)=a1*b1*(c1-c0)

Этот способ примен. для мультипликативных моделей. Правило махания рук: все слева от отчетного периодв фиксируется на фактическом уровне, справа – на базисном.

13. Методы детерминированного ФА (м. взвешенных конечных разностей, логарифмический м., интегральный м.)

М. взвешенных конечных разностей

Влияние каждого фактора оценивается по всем возможным вариантам подстановок и нахождение среднего значения.

у=a*b*c*d

	Варианты (n!) подстановок	∑∆у( )	∑∆у( )/n!
∆y(a)	a*b*c*d,b*c*d*a …	∑∆у(а)	∑∆у(a)/n!
∆y(b)		∑∆у(b)	∑∆у(b)/n!
∆y(c)		∑∆у(c)	∑∆у(c)/n!
∆y(d)		∑∆у(d)	∑∆у(d)/n!

Достоинства метода: 1) дает точное разложение 2) не зависит от последовательности факторов  3)универсальный метод     Недостаток - трудоемкость

Логарифмический м.

Применяется для мультипликат. и кратных моделей

1)  мультипликат. модель y=a*b

                                 

             

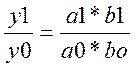
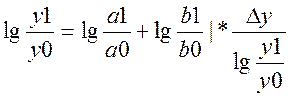
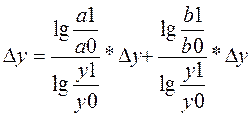
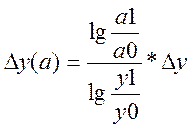
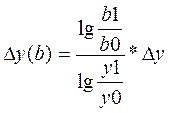
2)  кратная модель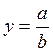

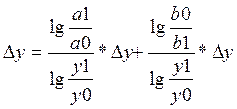
Интегральный м.

1) мультипликат. двухфакторная модель

y=a*b

∆y(a)= ∆a * b0 + ½*∆a*∆b=1/2*∆a*(b0+b1)

∆y(b)= ∆b * a0 + ½*∆a*∆b=1/2*∆b*(a0+a1)

2) кратная модель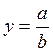

          

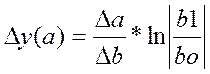
Достоинства метода: - самый точный

- не зависит от последовательности факторов

14. Последовательность проведения стохастического (корреляционного ФА)

1) Отбираются факторы, которые могут оказать существенное влияние на результативный показатель. Кол-во факторов включаемых в модель должно быть в 8-10 раз меньше, чем число единиц совок-сти. Изучение (или рассмотрение) характера связи между признаками. Не рекомендуется включ. в корреляц. модель линейного типа факторы, кот. связаны с результативным показателем. Выбор сущ. факторов, которые имеют коэф-нт корреляц. связи >0,8. Нельзя вкл. в модель мультиколинеарные факторы. 2) Исходная информация по каждому факторному и результативному показателю проверяется на достоверность, однородность и соответствие закону нормальн. распределения. 3) Изучается характер и моделируется связь между факторами и результат показателями. 4) Расчет основных показателей связи, а именно – самого уравнения связи; - коэф-тов регрессии, корреляции, детерминации. Коэф-нт регрессии показ. изменение результата при изменении фактора на единицу.

-уравнение регрессии.

15. СТОХАСТИЧ. ОЦЕНКА И ПРАКТИЧЕСКОЕ ИСПОЛЬЗ-Е РЕЗ-ТОВ КОРР. АНАЛИЗА

1. Для оценки эффективности использования производственного ресурсного потенциала предпр-ия.   Если   , то эффективность использования производственного потенциала Y i единицы совокупности выше, чем в среднем по совокупности. Если Y – c/c или затраты, то наоборот, эфф-ть ниже. Если U<0, эффект-ть использ-ния производственного потенциала i-предпр-ия ниже, чем среднее по совокупности. Через оценку эфф-ти использ-ния ресурсов предпр-ия косвенным образом оценивается уровень менедж-та, организации произв-ва.

2. Для оценки ресурсообеспеч-ти предпр-ия. Если  , то уровень обеспеч-ти ресурсами выше, чем в среднем по совокупности и наоборот. =ресурсообесп-ть + эфф-ть использ-ния ресурсов.

3. Для прогнозирования значения результативного показателя. Подставляя прогнозные значения факторов в уравнение, получаем прогноз результата. Различные уровни факторов дают разные прогнозные рез-ты: пессимистические (берутся min значения факторов), оптимистические/идеальные (самые лучшие знач факторн признаков), наиболее реальный.