Ответы на экзаменационные вопросы № 1-55 по дисциплине "Экономический анализ" (Предмет экономического анализа. Классификация видов анализа), страница 11

Для простейшего потока (Пуассоновский поток) частота наступления события подчиняется закону Пуассона, в соотв. с кот 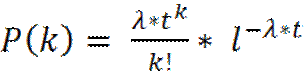. Р-вероятность того, что за произвольно выбранный период t поступит k требований.

– мат.ожидание случ.величины

λ – плотность входящего потока (кол-во событий в ед.времени).

28. Применение теории игр в анализе хоз.деятельности

Статист.т.и. явл-ся составной частью общей ТИ, кот. представляет собой раздел соврем.прикл.математики, изучающей методы обоснования оптим.решений в конфл.ситуациях. В ТИ различают понятия как игрок: природа – совокупность обст-ств, в условиях кот. приходится принимать решения второму игроку, кот. называют статистик – стремится выиграть игру у воображаемого противника природы.

Для статист. игры хар-на частичная неопределенность. Т.к. природа развивается и действует в соотв со своими объективно существующими законами.

На промышл п/п ТИ может использоваться 1. для выбора оптим.решений при создании рационал. запасов сырья, материалов, полуфаб. 2. вопросы кач-ва производ.продукции и др.экон.ситуациях.

Увеличение запасов, в т.ч. страховых или сокращ.запасов, кот. обеспечивают минимизацию затрат на их хранение.

Др. тенденция – стремление к выпуску продукции, ведущего к снижению труд.затрат, к повышению кач-ва, кот. сопровождается уменьшения кол-ва производимых изделий и увеличению трудовых затрат.

В с/х ТИ применяется при решении экон.задач, в кот. оппозиционной силой выступает природа, и когда вер-ть наступления событий многовариантна или неизвестна.

Применение ТИ на примере снижения цен на продукцию, кот не нашла покупателя

У п/п осталась нераспред. некот кол-во продукции, причем при установленной цене спрос  продукции отсутствует. Чтобы реализовать – надо понизить цену. Применение ТИ позволяет определить размер снижения цены, чтобы потери от реал. были мин.

Игрок 1(природа) – спрос на продукцию; природа может принимать разл.состояния: V=( V1; V2), V1 – малоэластичный, V2 – высокоэластичный.

Игрок 2(статистик) – п/п, у кот имеются разл.варианты снижения цены на продукцию(а1=20%, а2=30%, а3=40%, а4=50%).

Предполагается, что известна функция f=α(v;a), кот. выражает потери п/п, определяемые его действиями и состоянием природы V. Данная ф-ция α считается заранее заданной для всех возможных комбинаций или сочетаний этих величин и она задается с помощью матрицы потерь(матрицы игры). Каждый элемент матрицы потерь на основе данных: цена реал-ции ед. 20тыс.руб/ед; кол-во нереал.продукции 500шт.; решение п/п о снижении прод.цены 20,30,40,50%; предполагаемый объем продажи продукции в рез-те снижения цен определен. Состоянию природы соотв. 2 состояния:V1:

V2:

Матрица потерь L(V,a), тыс.руб.: