Рішення: Нехай мале джерело світла
перебуває у фокусі
лінзи Л1. Світлові промені після переломлення в лінзі Л1будуть паралельні оптичній осі, а після переломлення в
лінзі Л2
зберуться в її фокусі. Якщо відстань між лінзами значно менше фокусної відстані
кожної з лінз, то систему із двох лінз можна розглядати як тонку лінзу.
Застосовуючи тепер формулу тонкої лінзи до системи із двох лінз, одержимо ![]() або
або ![]() ,
де f – фокусна відстань системи із
двох лінз D – її
оптична сила.
,
де f – фокусна відстань системи із
двох лінз D – її
оптична сила.
|
|
|
Рис. 2.2.20 |
Приклад 19. З тонкої плоскопаралельної скляної пластинки виготовлені три лінзи (рис. 2.2.20). Виявилося, що фокусна відстань лінз 1 й 2, складених разом, f12 < 0; фокусна відстань лінз 2 й 3, також прикладених впритул один до одного, f23 < 0. Припускаючи, що лінзи тонкі, знайти фокусні відстані кожної із трьох лінз.
Рішення: Беручи до уваги, що оптичні сили тонких лінз, прикладених впритул один до одного складаються (див. рішення задачі), одержимо:
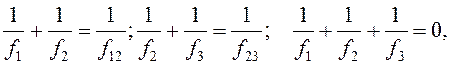
Останнє співвідношення випливає з того, що при додаванні всіх трьох лінз виходить система з нульовою оптичною силою – плоскопаралельна пластинка. Вирішуючи ці рівняння, знайдемо:
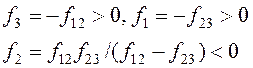
Приклад 20. Дві плоско-опуклі лінзи, будучи складені плоскими сторонами, утворюють лінзу з фокусною відстанню f1. Знайти фокусну відстань f2 лінзи, що вийде, якщо скласти ці лінзи опуклими сторонами, а простір між ними заповнити водою. Показники переломлення скла й води рівні п = 1,66 й nb = 1,33.
Рішення: Як відомо, оптична сила лінзи
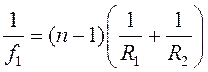 ,
,
де R1й R2 – радіуси кривизни опуклих поверхонь лінз. У другому випадку додається третя лінза
(водяна) з увігнутими поверхнями,
з радіусами
кривизни R1й R2 й оптичною силою 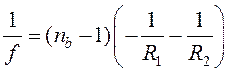 .
Загальна оптична сила дорівнює сумі оптичних сил складових лінз (див. рішення
завдання):
.
Загальна оптична сила дорівнює сумі оптичних сил складових лінз (див. рішення
завдання):
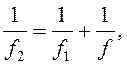 звідки
звідки 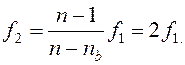
|
|
|
Рис. 2.2.22 |
Приклад 21. На рис. 2.2.22 зображена система із двох сферичних дзеркал: увігнутого З1 (радіус кривизни R1 = 20 м) і опуклого З2 (радіус кривизни R2 = 10 м), розташованих на відстані L = 5 м один від одного. Система призначена для тимчасової затримки короткого світлового імпульсу, що падає на дзеркало З1на відстані h = 20 см від оптичної осі у вигляді тонкого променя, паралельного осі. Через який час цей промінь вийде через отвір діаметра d=2 см, розташованого в центрі опуклого дзеркала?
|
|
|
Рис. 2.2.23 |
Рішення: З данних завдання
видно, що система конфокальна, тобто фокуси дзеркал З1й З2
збігаються. Отже, промінь, що йде до дзеркала З1паралельно оптичній
осі й після відбиття від нього по напрямку до фокуса, після відбиття від дзеркала З2
знову буде йти паралельно оптичній осі, але нижче (рис. 2.2.23). Так як ![]() , з подоби трикутників
одержуємо, що після першого відбиття
, з подоби трикутників
одержуємо, що після першого відбиття ![]() ,
а після n-го відбиття hn =h/2n.
Промінь вийде із системи,
коли
,
а після n-го відбиття hn =h/2n.
Промінь вийде із системи,
коли ![]() ;
звідси одержуємо
;
звідси одержуємо ![]() ,
, ![]() , тобто промінь вийде із системи після п'яти відбиттів. Він пройде в системі шлях l = 9L і час
затримки променя в системі
, тобто промінь вийде із системи після п'яти відбиттів. Він пройде в системі шлях l = 9L і час
затримки променя в системі ![]() с.
с.
Приклад 22. Об'єктив зорової труби має фокусну відстань ![]() см, а окуляр
см, а окуляр ![]() см. Труба встановлена на нескінченність. У якому місці
потрібно поставити діафрагму, щоб поле зору було різко обмежене? Який кут поля
зору, якщо діаметр діафрагми D= 12 мм? Яке кутове збільшення труби?
см. Труба встановлена на нескінченність. У якому місці
потрібно поставити діафрагму, щоб поле зору було різко обмежене? Який кут поля
зору, якщо діаметр діафрагми D= 12 мм? Яке кутове збільшення труби?
Рішення: У трубі, встановленій на нескінченність, відстань між об'єктивом й окуляром
дорівнює сумі ![]() . Перше зображення вилучених предметів розташовується в загальній фокальній площині
об'єктива й окуляра; у цій площині й варто розташувати діафрагму поля зору.
Розмір діафрагми визначає кут
поля зору. Він дорівнює
. Перше зображення вилучених предметів розташовується в загальній фокальній площині
об'єктива й окуляра; у цій площині й варто розташувати діафрагму поля зору.
Розмір діафрагми визначає кут
поля зору. Він дорівнює ![]() . Беручи до уваги малість кута а, можна записати
. Беручи до уваги малість кута а, можна записати ![]() . Паралельний пучок світла, що
входить в об'єктив під кутом a, вийде з
окуляра під кутом
. Паралельний пучок світла, що
входить в об'єктив під кутом a, вийде з
окуляра під кутом ![]() . Кутове
збільшення
. Кутове
збільшення 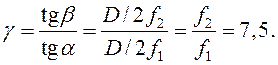
Примітка. Око має значну область акомодації. У нормального людського ока ця область простирається від відстані близько 10 см нескінченно. У тих випадках, коли очі озброєні зоровим приладом (окуляри, лупа, мікроскоп, зорова труба), уявне зображення предмета, розглянуте оком, повинне, звичайно, розташовуватися в області акомодації.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.