Основи захисту відеоінформації: Методичний посібник до практичних занять. Частина 1, страница 29

Рішення: Нехай х – відстань від предмета до зображення, тоді відстань від лінзи до зображення . Скористаємося формулою лінзи . Після перетворення одержуємо:

З огляду на те, що f, а й х – дійсні величини, одержуємо . Зображення дійсне; отже, f > 0 і x > 0. Тому , а . Відповідно маємо .

Приклад 7. Відстань між точковим джерелом світла й екраном дорівнює L. Лінза, поміщена між ними, дає на екрані чітке зображення при двох положеннях, відстань між якими дорівнює l. Визначити фокусну відстань лінзи.

Рішення:.

Приклад 8. Відстань по осі між предметом і його прямим зображенням, що дають лінзою, l = 5 см. Лінійне збільшення b = 0,5. Визначити фокусну відстань лінзи.

Рішення:  см.

Приклад 9. За допомогою лінзи на екрані отримане зображення предмета зі збільшенням b₁ = 2. Яке буде збільшення, якщо відстань між предметом й екраном збільшити в 1,6 рази?

Рішення: Збільшення . Тому що , одержимо , а . Вирішуючи це квадратне рівняння, знаходимо два рішення: .

Приклад 10. Освітлювач, призначений для одержання спрямованих світлових пучків, складається із точкового джерела світла й лінзи діаметра D = 6 см з фокусною відстанню f = 15 см. На якій відстані від лінзи повинне бути розташоване джерело щоб промені, що пройшли через лінзу, утворили на екрані світлову пляму діаметром d=4 см? Відстань від лінзи до екрана L=100 см.

Рішення: З рис. 2.2.9 видно, що можливо два рішення. Якщо зображення джерела виходить за екраном (S₁), то , звідки . По формулі лінзи

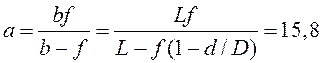 см.

У другому випадку одержуємо 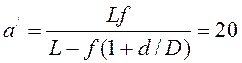 см.

Приклад 11.Точкове джерело світла розташоване на відстані а= 30 см від лінзи, що збирає, оптична сила якої D= 5 дптр. На яку відстань зміститься зображення джерела, якщо між лінзою й джерелом помістити товсту скляну пластинку товщиною L= 15 см з показником переломлення n = 1,57?

Рішення: Під час відсутності скляної пластинки відстань від лінзи до зображення b =a/(a—1) = 60 см, де  – оптична сила лінзи. Розглянемо тепер переломлення променів у пластинці. Як видно з рис. 2.2.10, вертикальний зсув променя, що прошла через пластинку, , де a і b – кути падіння й переломлення; звідси:

.

Для малих кутів a і b відношення тангенсів можна замінити відношенням синусів: . Таким чином, , . Шукана відстань l між зображеннями дорівнює :

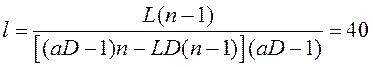 см.

Приклад 12. Лінза, що збирає, Л дає в S₁ точці дійсне зображення джерела S, розташованого на оптичній осі лінзи (рис. 2.2.11). Між лінзою Л₁ и зображенням S₁поставлена розсіювальна лінза Л₂, положення фокусів якої задані. Знайти побудовою нове положення зображення джерела. Розглянути випадок, коли відстань між S₁ і Л₂ більше фокусної відстані лінзи Л₂.

Рішення: Проведемо допоміжний промінь aa' паралельно променю ВР через оптичний центр лінзи Л₂ (рис. 2.2.12) Промінь aa' повинен перетнути продовження переломленого променя CD у фокальній площині ff'^' лінзи Л₂. Таким чином, уявне зображення джерела S буде перебувати в точці S₂. Як видно з побудови на лінзу Л₂ падає збіжний в S₁пучок променів. У подібних випадках прийнято говорити, що S₁ грає для лінзи Л₂ роль "уявного" джерела.

Приклад 13.Лінза, що збирає, Л дає в точці S₁ дійсне зображення точкового джерела S, розташованого на оптичній осі лінзи (рис. 2.2.13). Між джерелом S і лінзою Л₁поставлена ще одна лінза, що збирає Л, положення фокусів якої задані. Знайти побудовою нове положення зображення джерела. Розглянути випадок, коли відстань між S і Л₂ менше фокусної відстані лінзи Л₂.

Рішення: Звичайною побудовою допоміжного променя aa', паралельного променю АВ, знайдемо напрямок переломленого променя ВР (рис. 2.2.14). Далі, побудовою, аналогічним розгляну­тому в прикладі 12, визначимо положення фокальної площини лінзи Л₁, напрямок переломленого променя CD і тим самим положення зображення S₂.