Основи захисту відеоінформації: Методичний посібник до практичних занять. Частина 1, страница 28

У дифракційній решітці максимуми світла спостерігаються в напрямках, що становлять із нормаллю до решітки кут j, що задовольняє наступному співвідношенню (за умови, що світло падає на решітку нормально):

де d – постійна решітка, j – кут дифракції, l – довжина хвилі й k – порядок спектра.

Приклади рішення завдань

Приклад 1. На рис.2.2.1 зображене точ­кове джерело світла S, його зображення S₁ отримане за допомогою лінзи, і оптична вісь лінзи OO₁. Визначити побудовою положення лінзи й знайти її фокус. Дійсне або уявне це зображення?

Рішення: Пряма SS₁ перетинає оптичну вісь OO₁(в оптичному центрі лінзи, тому що через цю точку промінь проходить не переломлюючись (рис. 2.2.2). Отже, знайдене положення лінзи а, крім того, тепер уже видно, що зображення уявне, пряме й зменшене; отже, лінза розсіююча.

Щоб знайти положення її фокуса, проводимо пряму SA || OO₁. Після переломлення в лінзі її продовження повинне проходити через точку S₁. Точка перетинання AS₁ з OO₁й є головний фокус лінзи.

Приклад 2. На рис. 2.2.3 зображено хід променя ABC через розсіювальну лінзу. Визначити побудовою фокус.

Рішення: Проведемо допоміжний промінь аа^!, що проходить через оптичний центр лінзи паралельно променю АВ (рис. 2.2.4). Продовження промення ВР перетинається із променем аа' у фокальній площині лінзи ff^'. Точка F – головний фокус лінзи.

Приклад 3. На рис. 2.2.5 зображено хід променя ABC через лінзу, що збирає. Побудувати хід довільного променя DE. Розглянути випадки, коли точка перетинання променів АВ й DE лежить ліворуч і праворуч від лінзи.

Рішення: Спочатку побудовою допоміжного променя аа', паралельного АВ, визначимо положення фокальної площини ff^' (рис. 2.2.6). Потім за допомогою допоміжного променя bb', паралельного DE, визначимо напрям переломленного променя EF. Випадок, коли точка перетинання променів АВ й DE лежить праворуч від лінзи.

Приклад 4. На рис. 2.2.7 зображене точкове джерело світла S, його зображення S₁, отримане за допомогою лінзи, що збирає, і найближчий до джерела фокус лінзи F. Відстані SF =l й SS₁ =L задані. Визначити положення лінзи і її фокусну відстань.

Рішення: Відстань від джерела S до лінзи

;

фокусна відстань

.

Приклад 5. За допомогою лінзи, що збирає, одержують зображення двох точкових джерел А і В. Джерело А розташоване на оптичній осі на подвійній фокусній відстані від лінзи; джерело В зміщено від осі на невелику відстань так, що лінія, що з'єднує обидва джерела, утворить із оптичною віссю кут j = 30° (рис. 2.2.8). Під яким кутом до оптичної осі варто розташувати плоский екран, щоб одночасно одержати на ньому чіткі зображення обох джерел?

Рішення: Побудуємо зображення джерел А і В. Зображення джерела А буде перебувати на головній оптичній осі в точці А' на відстані 2f від лінзи. Побудова зображення джерела В зрозуміла з рисунку. Шуканий кут визначається зі співвідношення , де у і b – відстані від зображення В' до головної оптичної осі й до лінзи. З іншого боку, , де х и а – відстані від джерела В до головної оптичної осі й до лінзи. З подоби трикутників ВСО й В'С'О маємо . По формулі лінзи , звідки b=af/(a–f). Використовуючи ці рівняння, знаходимо

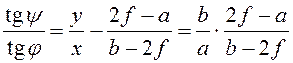
Підставляючи вираження для b, одержимо . Отже, y= 30°. Отже, якщо розташувати екран під кутом 30° до головної оптичної осі так, щоб він перетинав головну оптичну вісь у точці, що знаходиться на відстані 2f від лінзи, то зображення обох джерел будуть чіткими.

Приклад 6. На якій відстані а від лінзи, що збирає, треба помістити предмет, щоб відстань між предметом і його дійсним зображенням було мінімальна? Фокусна відстань лінзи дорівнює f.