Другие предметы \ Теория автоматического управления

Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 9

; ;	(2.16)
; ,	(2.17)

где - пространственная координата объекта в системе координат, в центре которой находится устройство, измеряющее расстояние до объекта:

;

(2.18)

, - скорость движения объекта и управляющее воздействие, недоступные прямым измерениям; - возмущающее воздействие, которое является неизвестной функцией пространственной координаты ; - постоянная времени объекта; - случайная погрешность измерений с дисперсией .

Объект (2.16)-(2.18), имеющий постоянную времени с., движется под действием управляющего и возмущающего воздействий, изменения которых приведены на рисунках 4 и 5.

Наблюдателю известна оценка постоянной времени с. На рисунке 6 изображен график изменения скорости движения объекта. На рисунке 7 приведены результаты измерений текущих значений пространственной координаты этого объекта.

Текущие значения пространственной координаты, измеренные с относительной погрешностью , использовались для оценивания текущих значений скорости движения объекта (одновременно с идентификацией постоянной времени) с помощью алгоритма рекуррентного МНК (фильтра Калмана) и ПИ-регулятора (2.10)-(2.15).

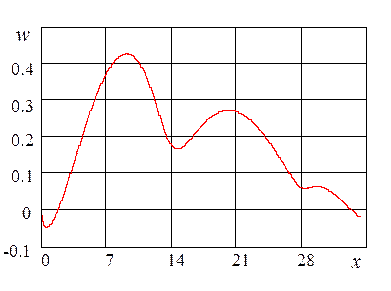
Рис. 4. Изменение возмущающего

воздействия вдоль пространственной

координаты

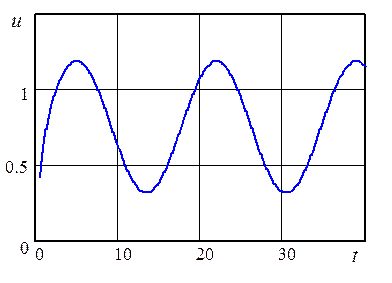
Рис. 5. Изменение управляющего

воздействия во времени

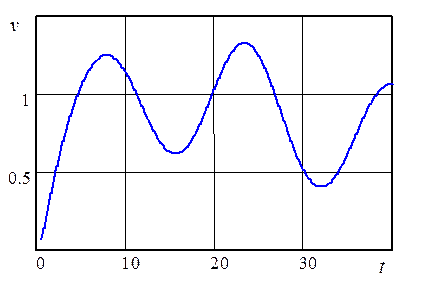
Рис. 6. Изменение скорости

движения объекта во времени

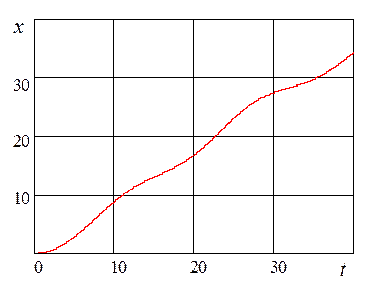
Рис. 7. Изменение во времени

выходного сигнала измерительного

устройства

Результаты моделирования приведены на рисунке 8. Линией 1 на этом рисунке изображен график изменения скорости движения объекта.

Из графиков, изображенных на рисунке 8, видно, что в этом примере алгоритм (2.10)-(2.15) обеспечивает несмещенные оценки скорости движения объекта (линия 2) со среднеквадратическим отклонением погрешности оценивания . В то же время оценки фильтра Калмана (линия 3 на рис. 8) имеют существенное смещение ().

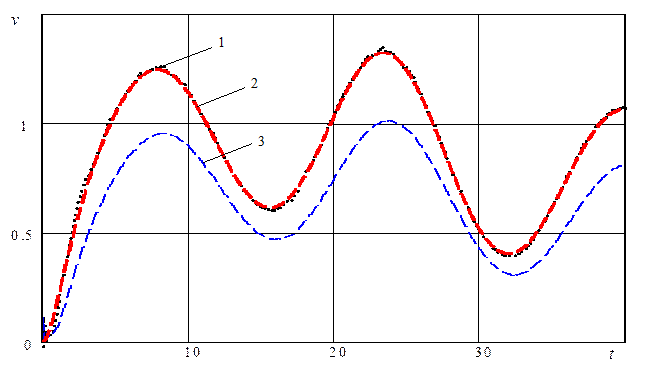
Рис. 8. Результаты оценивания скорости движения объекта

Пример 2. Сравниваются три системы автоматического управления нелинейным объектом, который имеет следующие уравнения состояния:

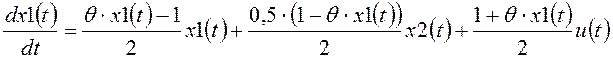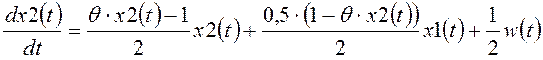где параметр .

В первой (оптимальной) системе управления использовались оптимальное управляющее воздействие (рис. 9) и известное возмущающее воздействие

В процессе имитационного моделирования угол фазового запаздывания принимал в случайные моменты времени случайные значения из диапазона [‑π; π]. При этом частоту колебаний выбирали случайным образом из диапазона [0,01; 10].

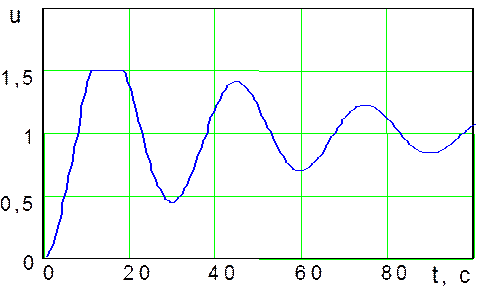
Рис. 9. Оптимальное управляющее воздействие

Система управления № 2 реализует алгоритм (2.10)-(2.15) с использованием следующей информации:

множество допустимых возмущающих воздействий задано неравенствами ;

множество допустимых управляющих воздействий задано неравенствами

;

известно точное значение параметра ;

в момент времени с заданы допустимые значения переменной состояния и скорости изменения во времени этой переменной:

, ;

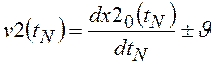ограничения на переменную заданы нелинейным уравнением:

где - погрешность измерений текущих значений сигнала (погрешность измерений является случайным процессом с дисперсией и временем корреляции с);

выходной сигнал измерительного устройства связан с переменными состояния объекта управления нелинейным уравнением , где - вектор случайных погрешностей измерений, которые имеют нулевые средние значения, время корреляции с и дисперсию .