Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 11

Из структурной схемы нейрона (рис. 20) следует, что

Из уравнения (2.23) исключим переменную , используя для этого выражение (2.22). В результате получим следующее уравнение состояния -го нейрона скрытого слоя

где:

;  .

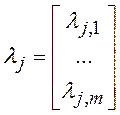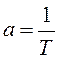Систему уравнений (2.24) для нейронов скрытого слоя представим в матричной форме

где:

Следовательно, выражение (2.26) является матричным уравнением состояния нейронов скрытого слоя для вектора переменных состояния , в которое входят настраиваемые параметры ,  и  и возмущающие воздействия .

Таким образом, нейрон скрытого слоя, состояние которого описывают уравнением (2.24), является динамической системой с настраиваемыми параметрами, структурная схема которой изображена на рисунке 21.

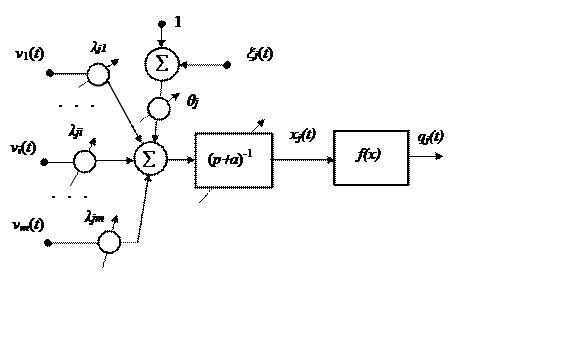
Рис. .21. Структурная схема нейрона  скрытого слоя (2.24)

Математическая модель нейронов входного слоя. Из формулы (2.25) видно, что нейрон входного слоя должен содержать параллельное соединение пропорционального и дифференцирующего звеньев. Однако операция дифференцирования сигналов, полученных экспериментально, является некорректно поставленной. Поэтому в нейронах входного слоя следует применять регуляризованную модель дифференцирующего звена.

Регуляризацию предлагается осуществить с помощью аппроксимации входных сигналов нейронов  В‑сплайнами, заданными с помощью тригонометрических функций [30]

где  - В-сплайн нулевого порядка:

 - периодическая функция времени с периодом  (рис. 22):

a,  - настраиваемые параметры нейрона входного слоя;  - погрешность аппроксимации.

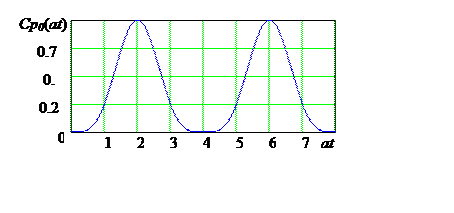
Рис. 22. График функции

Функция  в интервале  совпадает (с погрешностью ±10^-6) с традиционным В-сплайном третьего порядка (заданным в этом же интервале полиномами третьей степени [30]). Поэтому преобразование (2.29)-(2.31) следует рассматривать как способ задания В-сплайнов третьего порядка с помощью тригонометрических функций.

Предлагаемый способ задания В-сплайнов отличается от традиционного способа [32, 33] тем, что периодическая функция  всюду, кроме моментов времени  (где ), отлична от нуля и непрерывно зависит от параметра . Это позволяет  включать параметр  (частоту колебаний) в число настраиваемых параметров математической модели объекта управления. Традиционные В-сплайны, заданные полиномами, отличны от нуля только внутри интервала непрерывности сплайна. В математическое описание традиционных В-сплайнов длину интервала непрерывности сплайна  включают с помощью условных операторов. Поэтому в задачах аппроксимации длину интервала непрерывности В-сплайна  фиксируют, либо выбирают методом перебора [32].

Из формул (2.25), (2.29)-(2.31) следует, что

Таким образом, получена математическая модель нейронов входного слоя в виде системы уравнений (2.29)-(2.33), которые содержат подлежащие настройке параметры a и .

Математическая модель нейронов выходного слоя. В выходном слое используются нейроны, структурная схема которых изображена на рисунке 23.

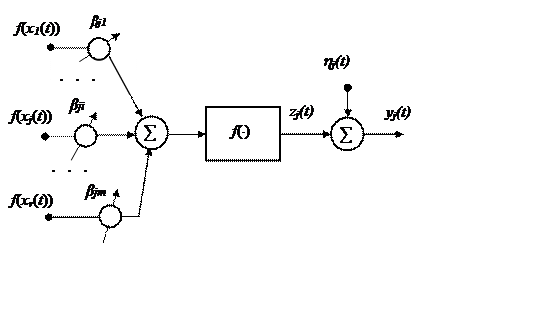
Рис. 23. Структурная схема нейрона  выходного слоя

Из структурной схемы (рис. 23) следует, выходной сигнал  -го нейрона выходного слоя связан со своими входными сигналами  уравнением

где  - функция активации нейрона;  - параметры нейрона, подлежащие настройке.

Алгоритм настройки параметров нейронов входного слоя.Настройку параметров  и  математической модели нейрона входного слоя (2.32), (2.33) будем осуществлять минимизацией среднеквадратического отклонения сигнала рассогласования

между измеренными значениями входного сигнала  и их оценками, вычисленными по математической модели (2.29)-(2.31).