При функционально-множественном подходе также может применяться большое разнообразие критериев. Здесь доминирующим является квадратичный критерий или квадратичная форма от ошибки прогнозирования [23-26, 31]. Для уменьшения влияния внешних возмущений в функционал могут вводиться различные взвешивающие функции [27, 30, 32]. В [19] при формировании функции потерь учитывалось влияние среды за счет задания статистических характеристик помехи. В [30] предложен функционал, который позволяет учесть ограничения, накладываемые на объект. Для этого в критерий вводится функциональное ограничение, отражающее априорные и апостериорные сведения о системе «объект + среда». Тем самым на этапе формирования критерия в него закладывается структура синтезируемого алгоритма. Другой подход к синтезу алгоритмов параметрического оценивания основан на применении стандартного квадратичного критерия (локального) [18], а процедура идентификации формируется на этапе учета имеющейся информации (априорной или предварительно обработанной), исходя из условия устойчивости системы.
Задачу выбора критерия адаптивного управления, наиболее полно учитывающего реальные условия функционирования объекта, исследовал А. А. Фельдбаум. Он показал, что идентификацию модели многомерного объекта в условиях неопределенности необходимо выполнять с учетом информации обо всех прошлых, текущих и будущих состояниях объекта и обучаемой модели. Эту информацию следует формировать в процессе обучения, используя результаты измерений входных и выходных сигналов объекта, доступных наблюдениям [34].
Поэтому для обучения модели объекта в качестве критерия идентификации будем использовать обобщенный квадратичный функционал в виде регуляризованного функционала обобщенной работы (ФОР), который составляют следующим образом.
Информацию о текущем состоянии объекта и обучаемой модели этого объекта содержит вектор сигналов рассогласования
|
|
(1.15) |
В скользящем временном
окне (протяженностью ![]() ) сформируем скалярную переменную
) сформируем скалярную переменную
![]() , образованную нормированной суммой средних
абсолютных значений сигналов рассогласования:
, образованную нормированной суммой средних
абсолютных значений сигналов рассогласования:
|
|
(1.16) |
где
|
|
(1.17) |
Новая переменная ![]() содержит в явном виде информацию о прошлых
состояниях объекта и его модели. Из (1.16) видно, что для этой переменной можно
составить нелинейное дифференциальное уравнение
содержит в явном виде информацию о прошлых
состояниях объекта и его модели. Из (1.16) видно, что для этой переменной можно
составить нелинейное дифференциальное уравнение
|
|
(1.18) |
с начальным условием
|
|
(1.19) |
где ![]() -
оценка вектора переменных состояния модели объекта, определенная в момент
времени
-
оценка вектора переменных состояния модели объекта, определенная в момент
времени ![]() .
.
Информацию о будущих состояниях объекта содержат скорости изменения выходных сигналов измерительных устройств. Поэтому дополнительное уравнение наблюдения будущих состояний объекта и его модели получим дифференцированием по времени правых и левых частей равенства (1.1) с учетом уравнения (1.13):
![]()
|
|
(1.20) |
Полученная регуляризованная модель объекта (1.1), (1.12)-(1.20) отличается от традиционных параметрических моделей тем, что:
1. На модель объекта действуют ограниченные по абсолютной величине возмущающие воздействия. Множество таких допустимых возмущающих воздействий можно формировать по алгоритму (1.10), либо алгоритму (1.9), (1.11), в которых используют сплайны.
2. Она содержит в явном виде информацию о прошлых, текущих и будущих состояниях анализируемого объекта и его модели.
3. Состояние модели объекта описывает система нелинейных дифференциальных уравнений (1.12)-(1.14). Модель наблюдения содержит систему нелинейных алгебраических и дифференциальных уравнений (1.1), (1.17)-(1.20).
Для составления критерия эффективности обучения сформируем вектор
![]() ,
,
а уравнения (1.12)-(1.14) представим в следующем эквивалентном виде:
|
|
(1.21) |
Для системы обучения модели объекта (1.1), (1.15)-(1.21) с ограниченными по абсолютной величине возмущающими воздействиями составим регуляризованный функционал обобщенного метода наименьших квадратов (РМНК):
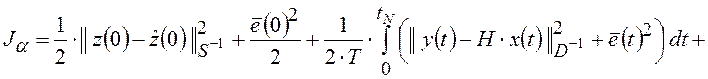
|
|
(1.22) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.