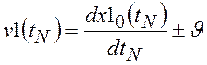Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 10

                    , .

Результаты имитационного моделирования системы управления № 2 приведены на рисунках 10-13.

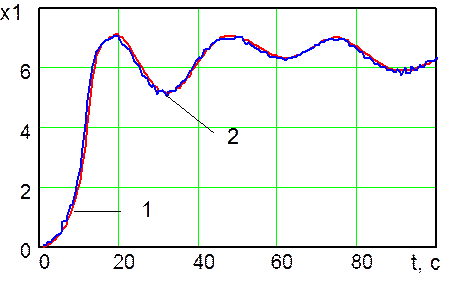
Рис. 10. Траектории изменения во времени переменной состояния , сформированные оптимальной системой управления (линия 1)

и системой управления № 2 (линия 2)

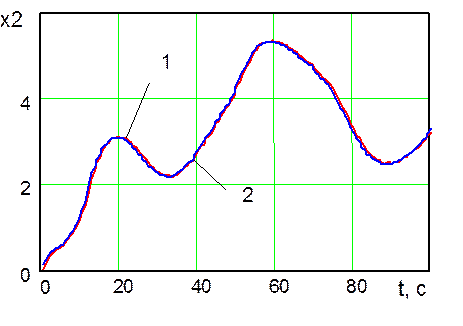
Рис. 11. Траектории изменения во времени переменной состояния , сформированные оптимальной системой управления (линия 1) и системой управления № 2 (линия 2)

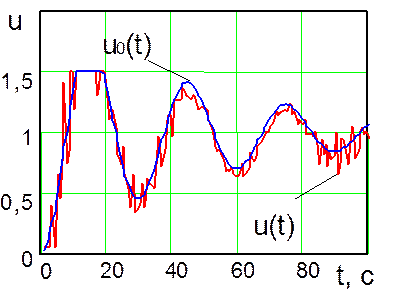
Рис. 12. Графики изменения во времени управляющего воздействия:  - оптимальное управляющее воздействие;  - управляющее воздействие, сформированное системой управления № 2

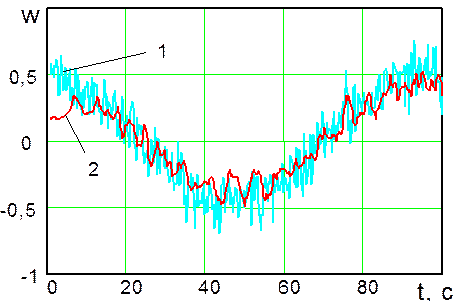
Рис. 13. Результаты идентификации возмущающего воздействия:

1 - действительный закон изменения во времени возмущающего

воздействия; 2 - оценка возмущающего воздействия, сформированная наблюдателем переменных состояния системы управления № 2

Результаты имитационного моделирования системы управления № 3 приведены на рисунках 14-17.

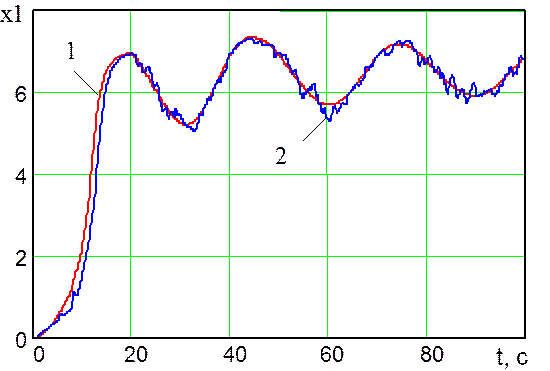
Рис. 14. Траектории изменения во времени переменной

состояния , сформированные оптимальной системой

управления (линия 1) и системой управления № 3 (линия 2)

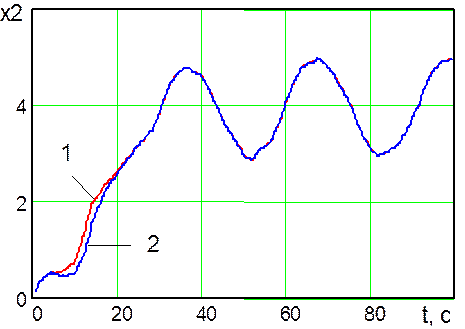
Рис. 15. Траектории изменения во времени переменной состояния , сформированные оптимальной системой управления (линия 1) и системой управления № 3 (линия 2)

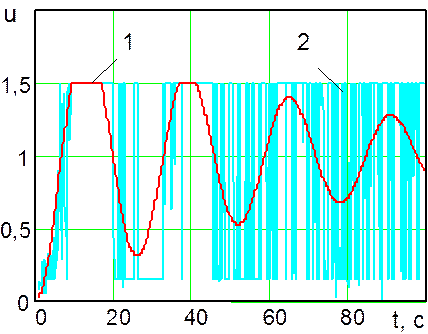
Рис. 16. Графики изменения во времени управляющего воздействия: 1 - управляющее воздействие, сформированное оптимальной системой управления; 2 - управляющее воздействие, сформированное системой управления № 3

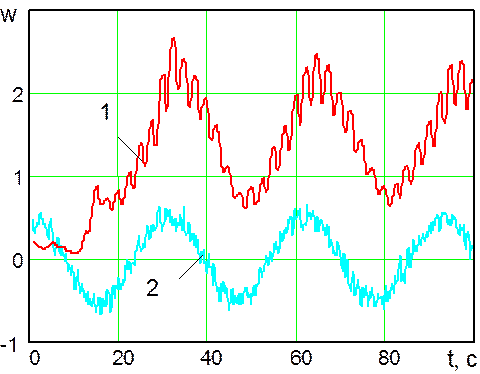
Рис. 17. Результаты идентификации возмущающего воздействия:

1 - оценка возмущающего воздействия, сформированная наблюдателем переменных состояния системы управления № 3; 2 - действительный закон изменения во времени возмущающего воздействия

Результаты имитационного моделирования показывают, что в рассматриваемом примере адаптивные системы автоматического управления, реализующие алгоритм (2.10)-(2.15), формируют переменные состояния объекта управления, близкие к своим оптимальным значениям. При этом система управления № 2, в которой используют точное значение параметра , формирует управляющее воздействие (рис. 12), близкое к оптимальному управляющему воздействию, и оценки возмущающих воздействий, близкие к своим действительным значениям (рис. 13).

Пример 3. Систему обучения модели ОУ (2.10)-(2.15) с ПИД-регулятором (2.16)  можно использовать для обучения многослойных нейронных сетей. Нейроны, входящие в один слой, имеют одинаковую структуру и соединены со всеми нейронами предыдущего слоя и всеми нейронами следующего слоя (рис. 18).

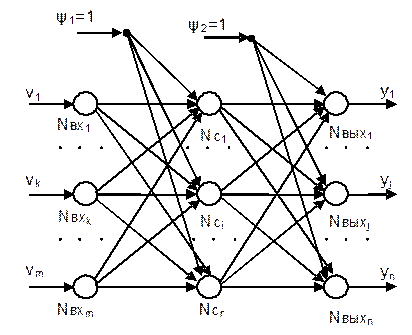
Рис. 18. Схема трехслойной нейронной сети

Покажем это на примере синтеза алгоритма обучения трехслойной нейронной сети, которая имеет  нейронов входного слоя,  нейронов скрытого слоя и  нейронов выходного слоя [35].

Предполагается, что обученная нейронная сеть в дальнейшем будет использоваться в качестве математической модели реального объекта, например, сети передачи информации. Обучение осуществляют с использованием эталонного объекта, к входам и выходам которого подключают обучаемую нейронную сеть и многомерный ПИД-регулятор настраиваемых параметров нейронной сети (рис. 19).

Для вывода алгоритма обучения необходимо составить уравнения состояния нейронов каждого слоя.

Рис. 19. Схема включения нейронной сети в систему обучения

Уравнения состояния нейронов скрытого слоя. Структурная схема нейрона приведена на рисунке 20, где  - функция активации нейрона;  - интенсивность потока данных, поступающих в нейрон из внешней среды в текущий момент времени .

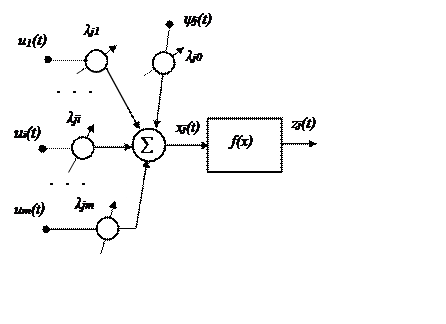
Рис. 20. Структурная схема нейрона скрытого слоя

Поток данных, поступающих на вход нейрона из внешней среды, может содержать случайные возмущения  и имеет среднее значение . Поэтому в системе обучения нейронной сети целесообразно использовать сглаженную оценку  интенсивности , вычисляемую по формуле:

,

(2.22)

где  - постоянная времени сглаживающего фильтра.

Предполагается, что по априорным данным известно, что случайные возмущения  могут принимать значения из интервала  с произвольным законом распределения вероятности (который не известен) и имеют нулевое среднее значение.