Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 5

Состояние объекта в текущий момент времени  определяют переменные состояния , объединенные в -мерный вектор переменных состояния . Доступные наблюдению переменные состояния, образующие -мерный вектор выходных сигналов объекта , связаны с вектором  выходных сигналов измерительных устройств уравнением наблюдения (в общем случае нелинейным):

где - прямоугольная матрица, с помощью которой формируют вектор выходных сигналов объекта  из переменных состояния ;  - вектор известных функций аргументов  и ;  - вектор погрешностей измерений.

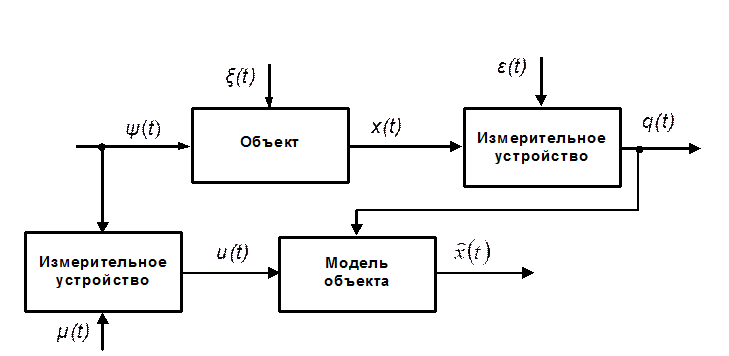
Рис. 1. Блок-схема системы идентификации модели объекта

Пространство входных переменных также можно разбить на два под­множества: входных сигналов , доступных измерениям, и переменных , изменяющихся по независимым от нас и в общем случае априори неизвестным причинам. Вектор входных сигналов  связан с вектором  выходных сигналов измерительных устройств уравнением

где  - вектор известных функций аргументов  и ;  - вектор погрешностей измерений.

Для измерительных устройств заданы пределы допустимых погрешностей измерений:

Причинно-следственные связи в объекте на множестве эксперимен­тальных данных можно описать в пространстве состояний с помощью дифференциального уравнения [15, 16, 30]:

где ,  - матрицы, известные с точностью до вектора параметров , принадлежащих ограниченной, но неизвестной об­ласти ;  - вектор неизвестных функций времени (вектор погрешностей линеаризации уравнения состояния). Параметры  могут быть постоянными или медленно изменяться с течением времени  неизвестным образом.

Формулы (1.1)-(1.4) определяют общую запись математической модели процессов, протекающих в объекте, представленной в пространстве состояний в параметрической форме. При этом уравнение (1.4) описывает эволюцию внутреннего состояния объекта (уравнение состояния), а уравнение (1.1) - процесс измерения (уравнение наблюдения). Из них можно получить различные виды пара­метрических представлений для нестацио­нарных, нелинейных и дискретных объектов (модель тренда, различные регрессионные модели, модель «вход-выход» и др.) за счет изменения или преобразования аргументов или вида используемых операторов [18]. Если  является белым шумом, то уравнение в (1.4) можно рассматривать как стохастиче­ское дифференциальное уравнение в форме Ито [16].

От непрерывных уравнений (1.1), (1.4) легко перейти к конечно-разностному представлению, (полагая , где ;  интервал съема данных) [16]:

Рассмотренные уравнения являются основой настраиваемых моделей,
применяемых в системах идентификации и управления. Настраиваемая
модель должна в каждый момент времени  вырабатывать прогноз выходной величины объекта на основе текущего множества экспериментальных
данных. Поэтому настраиваемую (адаптивную) модель часто называют
прогнозирующей. Близость параметров модели к параметрам объекта
служит признаком правильной (адекватной) работы модели.         

К настоящему времени существует огромное множество настраиваемых моделей (НМ). Выбор структуры НМ во многом является эвристическим процессом, практически не поддающимся формализации. Как отмечается в [17, 18], НМ должна формироваться на основе априорной информации. В [19] введено понятие оптимальной настраиваемой модели, минимизирующей второй момент невязки (ошибки) между выходами модели и объекта.

1.2. Регуляризованная модель объекта в пространстве состояний

1.2.1. Регуляризованная модель возмущающих воздействий

Непрерывные функции  с ограничениями (1.1), образующие вектор , можно получить путем нелинейного преобразования

где  - известная граница области допустимых возмущающих воздействий;  - вспомогательная непрерывная функция. В свою очередь, нелинейное преобразование (1.7) можно аппроксимировать с любой требуемой точностью аналитическими функциями переменной , либо функциями  с непрерывными первыми производными по этой переменной (сплайнами). В частности, подбором параметров  можно с требуемой точностью обеспечить выполнение равенства [30]