Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 6

Для аппроксимации неравенств (1.1) нелинейными равенствами можно применять и другие функции, например, дважды дифференцируемую функцию

.

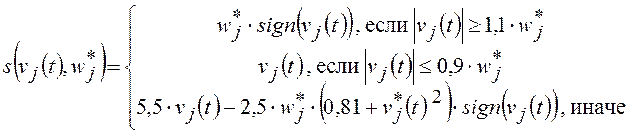График функции  при ,  и  приведен на рисунке 2.

Таким образом, с требуемой точностью неравенства (1.1.1) можно заменить нелинейными уравнениями, например, (1.7) (или (1.8)), которые в свою очередь можно представить в матричной форме:

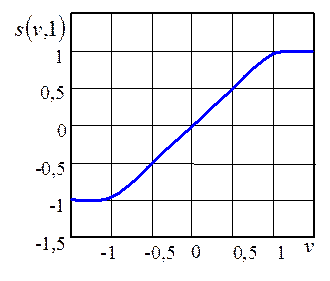
Рис. 2. График функции (1.8) с параметрами: ,  , ,

В скользящем временном окне, протяженностью , изменение во времени возмущающих воздействий можно приближенно описать с помощью сплайнов [17, 30, 32, 33]. В частности, путем варьирования величины временного окна  (интервала непрерывности сплайна), являющейся параметром регуляризации, можно обеспечить требуемую точность аппроксимации с помощью сплайнов нулевого порядка. Тогда оценки  вектора  возмущающих воздействий можно получить на выходе динамической системы (рис. 3):

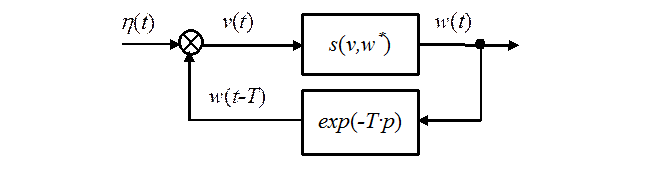
Рис. 3. Схема формирователя

допустимых возмущающих воздействий

Кроме того, можно применять систему со сглаживающим фильтром [30], например:

Если применяют сплайны первого порядка, то оценки вектора  вспомогательных функций , поступающих на вход нелинейного преобразователя (1.9), можно получить на выходе интегрирующего звена:

где  – вектор, образованный известными оценками  возмущающих воздействий  в момент времени ;  - вектор отклонений текущих значений возмущающих воздействий  от заданных сплайнами линий регрессии (вектор погрешностей аппроксимации).

1.2.2. Регуляризованная модель состояния объекта

С учетом формул (1.9) уравнение состояния объекта (1.4) принимает следующий вид:

При этом уравнение (1.13) следует дополнить математической моделью возмущающих воздействий (1.10), (1.11) (или (1.9), (1.12)) и уравнением эволюции во времени параметров:

Таким образом, с помощью сплайнов получены регуляризованные модели (1.10), (1.13) и (1.9), (1.12), (1.13), (1.14) объекта (1.4) с ограниченными по абсолютной величине возмущающими воздействиями.  При этом уравнениями (1.10) описывают кусочно-непрерывные возмущающие воздействия, а уравнения (1.9), (1.12) являются моделью непрерывных возмущающих воздействий. Параметром регуляризации является интервал непрерывности сплайнов [30, 31].

1.3. Критерий обучения модели объекта

Выбор критерия обучения модели объекта - один из важнейших этапов решения задачи идентификации. В системах идентификации применяется множество критериев в зависимости от подхода к задаче идентификации  [3, 4, 12-17, 23, 27-31]. Выбор критерия идентификации основывается на предпочтениях исследователя и отражает область его математических вкусов. Основное при выборе критерия - это возможность оценки качества аппроксимации (адекватности) модели объекту.

При статистическом подходе доминирующим является квадратичный критерий средних потерь от ошибки прогнозирования, так как он позволяет получить в аналитическом виде алгоритм адаптации. Такой подход является особенно важным для задач идентификации, сводящихся к получению рекуррентных алгоритмов оценивания. Кроме квадратичного функционала могут применяться также и другие виды нелинейных функционалов от ошибки прогнозирования (модульный, показательный, минимаксный и др.).

В информационной теории идентификации учет дополнительной ап­риорной информации приводит к формированию критерия в виде функционала, зависящего от наименее благоприятного распределения помехи. В [19] показано, что оптимальная функция потерь равна логарифмической функции правдоподобия с обратным знаком. При таком выборе оценки параметров объекта обладают максимальной асимптотической скоростью сходимости.