Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 12

Оценки настраиваемых параметров, обращающих в минимум критерий (2.35), можно вычислять, например, с помощью алгоритма рекуррентного МНК.

Алгоритм настройки параметров нейронов скрытого и выходного слоев. Выходной сигнал  эталонного объекта системы обучения нейронной сети (рис. 24) связан с переменными состояния  обучаемой нейронной сети (рис. 22) уравнением

где ,  - среднее значение и случайная составляющая погрешности обучения .

Сформируем вектор вспомогательных функций

,

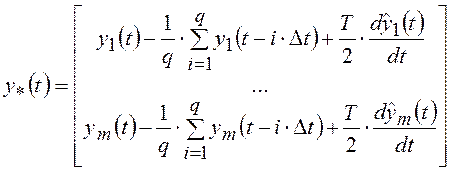который связан с вектором переменных состояния  обучаемой нейронной сети уравнением

где

 - известная в момент времени  оценка переменной ;  - вектор погрешностей обучения.

Поэтому настройку параметров  и  нейронов скрытого и выходного слоев можно осуществлять минимизацией критерия обобщенной работы

по переменным , ,  и  с учетом ограничений (2.26), (2.36)- (2.19), где  - матрица дисперсий погрешностей измерений выходных сигналов эталонного объекта, используемого для обучения нейронной сети.

Минимизация критерия обобщенной работы (2.40) с ограничениями (2.26), (2.36),  (2.38), (2.39) по переменным , ,  и  приводит к алгоритму самонастраивающегося ПИД-регулятора (2.10)-(2.15).

Правые части уравнений оценивания (2.10)-(2.15) содержат производные выходных сигналов эталонного объекта, используемого для обучения нейронной сети. Поэтому для уменьшения чувствительности оценок настраиваемых параметров к случайным возмущениям, которые могут содержать выходные сигналы эталонного объекта, целесообразно применять аппроксимацию этих сигналов В-сплайнами (2.29)-(2.31).

Оценка эффективности алгоритмов обучения нейронной сети. Традиционные алгоритмы обучения нейронных сетей, базирующиеся на алгоритме обратного распространения ошибки в сочетании с методом наискорейшего спуска [36] или в сочетании с рекуррентным методом наименьших квадратов (фильтром Калмана) [37], реализуют пропорциональный закон регулирования оценок настраиваемых параметров. Поэтому они формируют несмещенные оценки этих параметров только в том случае, когда возмущающие воздействия являются белыми шумами. Алгоритмы обучения нейронных сетей, базирующиеся на алгоритме обратного распространения ошибки в сочетании с методом скоростного градиента [36] реализуют пропорционально-дифференцирующий закон регулирования оценок настраиваемых параметров. Поэтому они обеспечивают более высокую скорость обучения, но имеют высокую чувствительность к случайным возмущениям.

Предлагаемый алгоритм обучения нейронной сети осуществляет путем ПИД-регулирования параметров нейронов скрытого и выходного слоев. Поэтому, как это известно в теории автоматического регулирования, он должен формировать несмещенные оценки настраиваемых параметров, иметь меньшую чувствительность к случайным возмущениям и обеспечивать более высокую скорость обучения по сравнению с традиционными алгоритмами. Сглаживание В-сплайнами [32] функций, используемых для обучения нейронной сети, дополнительно уменьшает чувствительность настраиваемых параметров к случайным возмущениям.

Количественный анализ указанных свойств разработанного алгоритма обучения нейронных сетей был выполнен путем сравнения его характеристик с аналогичными характеристиками наиболее распространенных алгоритмов в задаче обучения трехслойной нейронной сети, состоящей из одного нейрона входного слоя, трех нейронов скрытого слоя и одного нейрона выходного слоя. На вход этой сети подавали сигнал, увеличивающийся во времени и содержащий случайные возмущения с разными значениями времени корреляции и величины отношения сигнал/шум (ОСШ). Требовалось настроить параметры этой нейронной сети таким образом, чтобы ее входной сигнал уменьшался во времени по экспоненте. Для настройки параметров  использовался выходной сигнал эталонного объекта, искаженный случайными возмущениями при разных значениях времени корреляции и величины отношения сигнал/шум. Время корреляции (в секундах) возмущающих воздействий выбирали случайным образом из диапазона [0,01; 0,1], а величину отношения сигнал/шум выбирали случайным образом из диапазона [10; 30].