Разработка и анализ обучаемых моделей для систем автоматического управления и диагностики технического состояния технологических процессов, страница 13

Обучение этой нейронной сети осуществляли с помощью разработанного алгоритма, традиционного алгоритма обратного распространения ошибки [30]‑[32], алгоритма скоростного градиента [36] и фильтра Калмана [37]. Результаты обучения при времени корреляции шумов с., отношении входной сигнал/шум ОСШ=20дБ и отношении выходной сигнал/шум ОСШ=10дБ приведены на рисунках 24-29.

Графики изменения входного сигнала и обучающей выборки, полученные при времени корреляции шумов с, отношении (входной сигнал)/шум ОСШ=20дБ и отношении (выходной сигнал)/шум ОСШ=10дБ приведены на рисунках 24 и 25 соответственно.

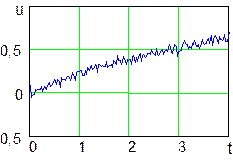
Рис. 24. Изменение во времени входного сигнала обучаемой

нейронной сети

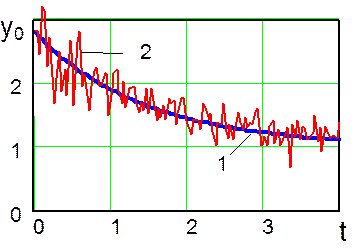
Рис. 25. График требуемого изменения во времени выходного

сигнала обучаемой нейронной сети (линия 1) и обучающая

выборка (линия 2)

На рисунках 26 и 27 представлены результаты обучения нейронной сети с помощью традиционного алгоритма обратного распространения (рис. 26) и с помощью алгоритма скоростного градиента.

Рис. 26. Выходной сигнал нейронной сети, обученной с помощью

традиционного алгоритма обратного распространения (линия 2) и

график требуемого изменения во времени выходного сигнала обучаемой нейронной сети (линия 1)

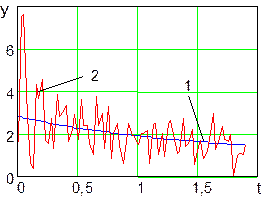
Рис. 27. Выходной сигнал нейронной сети, обученной с помощью

алгоритма скоростного градиента (линия 2) и график требуемого

изменения во времени выходного сигнала обучаемой нейронной сети (линия 1)

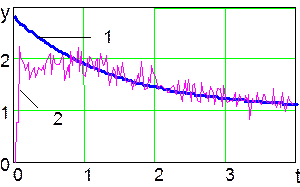
Рис. 28. Выходной сигнал нейронной сети, обученной с помощью

фильтра Калмана (линия 2) и график требуемого изменения во времени

выходного сигнала обучаемой нейронной сети (линия 1)

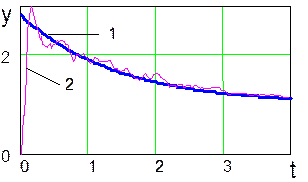
Рис. 29. Выходной сигнал нейронной сети, обученной с помощью

разработанного алгоритма (линия 2) и график требуемого изменения

во времени выходного сигнала обучаемой нейронной сети (линия 1)

Результаты имитационного моделирования показали, что в рассматриваемой задаче алгоритм обратного распространения ошибки оказался неустойчивым (рис. 26). Выходной сигнал нейронной сети, обученной с помощью алгоритма скоростного градиента, имеет высокую чувствительность к случайным возмущениям (рис. 27). Фильтр Калмана (рис. 28) уменьшает уровень случайного шума в выходном сигнале до 15 дБ и обеспечивает несмещенную оценку выходного сигнала нейронной сети при времени обучения с.

Выводы. В разделе 2 получен новый метод синтеза системы обучения регуляризованной модели (1.21) многомерного объекта с непрерывными ограниченными по абсолютной величине возмущающими воздействиями. Эта система обучения образована объектом управления, системой измерительных устройств обучаемой моделью объекта с многомерным ПИД-регулятором обучающих воздействий. Система обучения реализует регуляризованный алгоритм фильтра Калмана (2.10)-(2.15) для модели объекта с расширенным вектором переменных состояния.

Доказано, что система обучения модели объекта (1.21) устойчива и формирует несмещенные и состоятельные оценки переменных состояния объекта управления, оптимальные по регуляризованному критерию обобщенной работы (1.22), при любых значениях параметра регуляризации. Функционал (1.22) определяет суммарную нормированную энергию, которой обладали бы сигналы, образованные погрешностями аппроксимации возмущающих воздействий сплайнами первого порядка и сигналами рассогласования между выходными сигналами системы измерительных устройств и модели объекта. Требуемые значения частных показателей качества переходных процессов в системе обучения можно обеспечить выбором значений параметров регуляризации  и интервала непрерывности сплайнов . Функционал (1.22) совпадает с функцией стоимости критерия максимума апостериорной вероятности, если все возмущающие воздействия и погрешности измерений являются центрированными белыми гауссовскими шумами.