где ![]() -
интервал непрерывности сплайнов;
-
интервал непрерывности сплайнов; ![]() - матрица дисперсий погрешностей наблюдения
составляющих вектора
- матрица дисперсий погрешностей наблюдения
составляющих вектора ![]() ;
; ![]() ,
, ![]() -
параметры регуляризации, значения которых выбирают из интервала
-
параметры регуляризации, значения которых выбирают из интервала ![]() (например, с помощью метода невязки [32]);
(например, с помощью метода невязки [32]);
![]() -
положительно определенная матрица нормирующих множителей (например, известная
оценка дисперсий погрешностей аппроксимации возмущающих воздействий сплайнами);
-
положительно определенная матрица нормирующих множителей (например, известная
оценка дисперсий погрешностей аппроксимации возмущающих воздействий сплайнами);
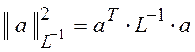 .
.
Функционал (1.22)
определяет взвешенную суммарную энергию, которой обладали бы сигналы,
образованные погрешностями задания начальных условий, сигналами рассогласования
![]() ,
, ![]() ,
, ![]() и погрешностями
и погрешностями ![]() аппроксимации
возмущающих воздействий сплайнами. Поэтому функционал (1.22) является
регуляризованным функционалом обобщенной работы (РФОР) системы обучения модели
объекта с вектором управляющих (обучающих) воздействий
аппроксимации
возмущающих воздействий сплайнами. Поэтому функционал (1.22) является
регуляризованным функционалом обобщенной работы (РФОР) системы обучения модели
объекта с вектором управляющих (обучающих) воздействий ![]() .
.
Кроме того, функционал (1.22) в явном виде учитывает информацию о прошлых, текущих и будущих состояниях системы обучения модели объекта, что полностью соответствует необходимым условиям построения адаптивных систем управления нелинейными объектами в условиях неопределенности, сформулированными в [34].
2. Обучение модели объекта в условиях неопределенности
2.1. Алгоритм обучения модели объекта в условиях неопределенности
Обучение модели состояния (1.1), (1.15)-(1.21) многомерного объекта (1.4) с ограниченными по абсолютной величине возмущающими воздействиями и неизвестными параметрами будем выполнять минимизацией функционала (1.22) при ограничениях (1.21). Эта задача условной оптимизации является частным случаем задачи оптимального управления нелинейным динамическим объектом со свободным правым концом. Для решения такой задачи оптимального управления можно применять принцип максимума.
В частности, Э. Сейдж и Д. Мелса [16] с помощью метода инвариантного погружения разработали алгоритм преобразования нелинейной двухточечной краевой задачи (возникающей при решении задачи оптимального управления со свободным правым концом) в задачу Коши. В соответствии с этим алгоритмом системе нелинейных дифференциальных уравнений
|
|
(2.1) |
|
|
(2.2) |
|
|
(2.3) |
с краевыми условиями
|
|
(2.4) |
эквивалентна
задача Коши для оценки ![]() вектора переменных состояния
вектора переменных состояния ![]() в форме уравнений нелинейного фильтра
Калмана:
в форме уравнений нелинейного фильтра
Калмана:
|
|
(2.5) |
|
|
(2.6) |
Принцип максимума в задаче минимизации функционала (1.22) при ограничениях (1.21) приводит к функции Гамильтона:
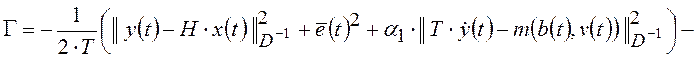
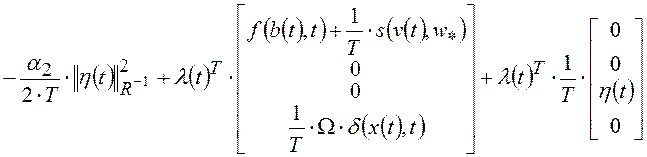 ,
,
где ![]() - вектор
неопределенных множителей Лагранжа. Поэтому оптимальное решение удовлетворяет
следующим уравнениям Эйлера-Лагранжа:
- вектор
неопределенных множителей Лагранжа. Поэтому оптимальное решение удовлетворяет
следующим уравнениям Эйлера-Лагранжа:
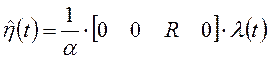 ;
;
|
|
(2.7) |
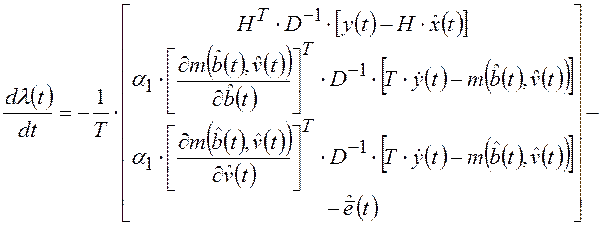
|
|
(2.8) |
с краевыми условиями
|
|
(2.9) |
Система уравнений (2.7)-(2.9) является частным случаем двухточечной краевой задачи (2.1)-(2.3), поэтому можно применять метод инвариантного погружения. При этом уравнения (2.5), (2.6) в рассматриваемом случае примут следующий вид:
![]()
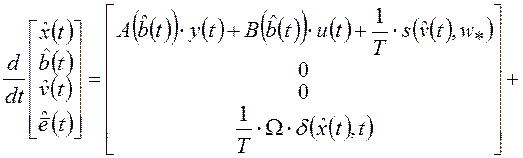
|
|
(2.10) |
||
|
|
(2.11) |
||
где:
|
|
(2.12) |
|
|
|
(2.13) |
|
|
|
(2.14) |
|
|
|
(2.15) |
|
Таким образом, оценки ![]() ,
, ![]() и
и ![]() векторов переменных состояния
векторов переменных состояния ![]() модели объекта, параметров
модели объекта, параметров ![]() и возмущающих воздействий
и возмущающих воздействий ![]() , оптимальные по регуляризованному функционалу
обобщенной работы (1.22), формирует регуляризованный фильтр Калмана (2.10)-(2.15).
, оптимальные по регуляризованному функционалу
обобщенной работы (1.22), формирует регуляризованный фильтр Калмана (2.10)-(2.15).
2.2. Анализ эффективности обучения модели объекта
Из сравнения уравнений (2.10)
и (1.19), (1.17), (1.18) следует, что оптимальную оценку ![]() вектора обучающих воздействий
вектора обучающих воздействий ![]() на модель объекта, оптимальную по критерию
(1.22), формируют по алгоритму
на модель объекта, оптимальную по критерию
(1.22), формируют по алгоритму
![]()
самонастраивающийся многомерный ПИД-регулятор. При этом матрицы переменных параметров этого ПИД-регулятора вычисляют в процессе обучения модели объекта по уравнению:
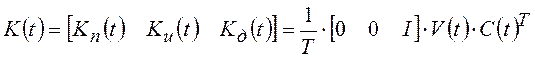 .
.
Пример 1. Нелинейный объект имеет уравнения состояния:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.