Задача дуального управления с функциональной адаптацией слишком сложна для практической реализации, так как не существует точной математической схемы, позволяющей учесть в алгоритме формирования управляющего воздействия все будущие значения возмущающих воздействий и все будущие значения переменных состояния нелинейных объектов управления. Дуальное управление можно реализовать только в нейтральных системах (в линейных системах и в нелинейных системах с возмущающими воздействиями в виде белых шумов, если оптимальные траектории заданы с точностью до белых шумов). Только в этих случаях оптимальные значения управляющих воздействий в текущий момент времени не зависят от будущих значений переменных состояния и будущих значений возмущающих воздействий. Поэтому в нейтральных системах управления справедлива теорема разделения задач оптимального оценивания переменных состояния и формирования оптимальных управляющих воздействий [5], [6], [7].
Существующая теория адаптивного управления базируется на принципе достоверной эквивалентности, в соответствии с которым при формировании оптимальных управляющих воздействий в системах управления вместо неизвестных переменных состояния и параметров можно использовать их оценки, найденные в процессе управления в результате анализа измеренных значений выходных сигналов ОУ. Координаты оптимальных (желаемых) траекторий перехода управляемых переменных в требуемое состояние должны быть заданы в явном виде или косвенно - с помощью критерия эффективности управления. Система управления, реализующая принцип достоверной эквивалентности, содержит объект управления (ОУ), систему измерительных устройств, формирователь управляющих воздействий и наблюдатель переменных состояния, включенный в цепь обратной связи (рис. 1.14).
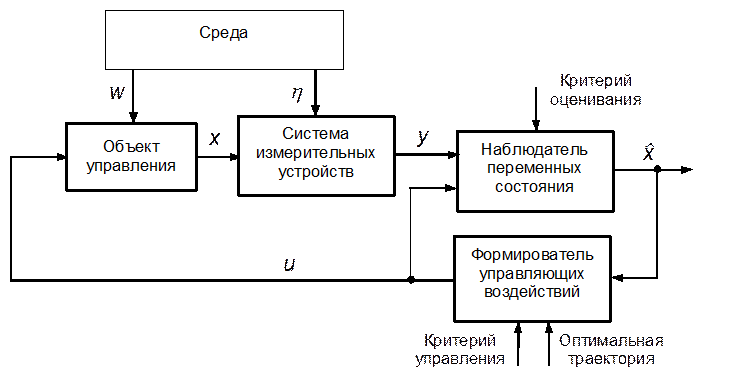
Рис. 1.14. Система адаптивного управления, реализующая
принцип достоверной эквивалентности
В задачах управления нелинейными объектами принцип достоверной эквивалентности выполняется, если математическое описание оптимальных траекторий перехода переменных состояния ОУ в заданное конечное состояние известно с точностью до параметров, а возмущающие воздействия являются аддитивными белыми гауссовскими шумами [5]. [7]. Однако в реальных системах, как правило, эти условия не выполняются. Так, например, системы связи и системы радионавигации используют нестационарные каналы связи с неизвестными параметрами и (или) переменными состояния, в которых действуют шумы с неизвестными функциями распределения вероятности [8]-[12]. Время корреляции шумов сопоставимо со временем корреляции информационного сообщения.
Оптимальная траектория перевода объекта управления из начального состояния в требуемое конечное состояние, как правило, не известна. Обычно известны лишь ограничения на множество допустимых траекторий перевода объекта управления из начального состояния в требуемое конечное состояние, заданные с помощью неравенств. Объект управления часто состоит из двух подсистем О1 и О2, при этом управляющие воздействия поступают на входы только подсистемы О1, а измерениям доступна другая часть переменных состояния ОУ. Поэтому в адаптивных системах управления используют приближенные методы, основанные на регуляризации исходной постановки задачи, например, с помощью метода регуляризации А.Н. Тихонова [13], [14]. При правильном применении метод регуляризации гарантирует получение приближенного решения регуляризованной задачи с точностью, достаточной для применения в инженерной практике [9].
В теории адаптивного управления сложились два подхода к описанию априорных неопределенностей математической модели системы управления: стохастический и детерминированный (минимаксный). Правильный выбор математической модели объекта управления является решающим условием, гарантирующим успех в решении задачи адаптивного управления. Этот выбор должен основываться как на понимании самой процедуры идентификации модели, так и на содержательной и формализованной информации об идентифицируемом объекте. Качество полученной модели может быть, в частности, оценено по критерию среднеквадратической ошибки, в котором множество проектных переменных включает структуру модели.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.