Разработка и исследование адаптивной системы управления активной мощностью гидроагрегата ГЭС с поворотно-лопастной турбиной, страница 13

В соответствии с этой теорией в цепь обратной связи системы управления включается обучаемая модель процессов формирования момента движущих сил турбины, активной мощности гидроагрегата и опорных траекторий перехода управляемых переменных в требуемое состояние. Полученная модель будет содержать нелинейные уравнения, описывающие комбинаторную зависимость, и неизвестные входные воздействия, подлежащие определению в процессе управления.

Выполненные исследования, в которых использовались реальные данные, полученные при пусках гидроагрегатов №№ 4, 8 и 19  ОАО «Волжская ГЭС», показывают, что с помощью предлагаемой системы можно уменьшить статическую погрешность регулирования активной мощности, снизить уровень вибраций и уменьшить расход воды через турбину, обеспечив в результате увеличение КПД гидроагрегата.

2  ИДЕНТИФИКАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИДРОАГРЕГАТА

2.1 Модель процесса формирования активной мощности

Теоретической и методологической основой предлагаемой системы адаптивного управления является способ управления сложными нелинейными объектами с ограниченными по абсолютной величине возмущающими воздействиями, разработанный в [8]. В соответствии с этой теорией в цепь обратной связи системы управления включают обучаемую математическую модель гидроагрегата, с помощью которой вычисляют оценки неконтролируемых возмущающих воздействий и параметров модели. Обученную модель используют для формирования управляющих воздействий.

Для разработки математической модели процесса формирования активной мощности использовались электронные архивы. В них сохранены значения переменных (сигналов датчиков, значений заданий регулятору) в дискретные моменты времени

 ;    ,

где  - шаг квантования времени.

Приращение активной мощности гидроагрегата за промежуток времени  определяют по уравнению баланса мощностей (рис.2.1):

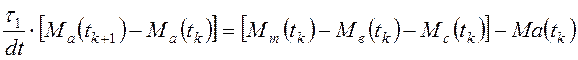,                 (2.1)

где:  - значение активной мощности генератора, подключенного к выделенной нагрузке;  - постоянная времени гидроагрегата;  - мощность турбины, величина которой зависит от углов установки лопаток НА  и лопастей РК  ;  - мощность, рассеиваемая на вертикальную вибрацию гидроагрегата;  - другие неконтролируемые потери мощности турбины в гидроагрегате.

Рис. 2.1. Модель процесса формирования активной мощности гидроагрегата

К настоящему времени не удалось определить аналитическую зависимость мощности турбины от углов установки лопаток НА  и лопастей РК   и зависимость мощности , рассеиваемой на вертикальную вибрацию гидроагрегата, от амплитуды вертикальной вибрации гидроагрегата . Поэтому эти зависимости определяют на первом этапе (предварительное обучение) с помощью В-сплайнов первого порядка [25]:

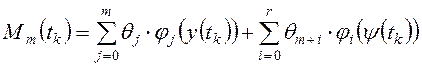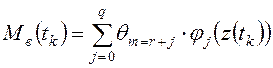;  ,   (2.2)

которые содержат неизвестные параметры  и известные функции  влияющего фактора. Функции  переменной  формируют по формулам:

;

 ;

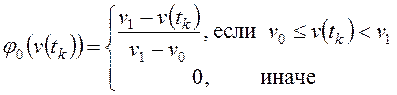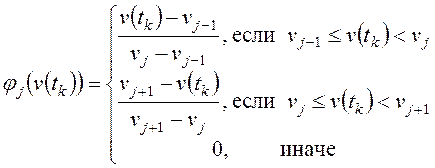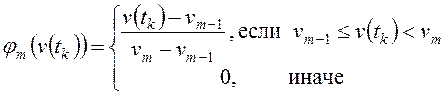.                                    (2.3)

После подстановки формул (2.2) и (2.3) в уравнение (2.1) получим модель процесса формирования активной мощности в следующем виде:

,        (2.4)

где  - возмущающее воздействие, создаваемое неучтенными факторами (погрешность модели).

Параметры , образующие вектор , определяют с помощью метода наименьших квадратов (МНК) с использованием результатов измерений активной мощности, уровня вертикальной вибрации, углов установки лопаток НА и лопастей РК в интервале времени .

Анализ точности модели (2.4) в разных режимах работы гидроагрегата выполнен в главе 4.

Уравнение (2.4) используется в разделе 2.5 при синтезе обучаемой модели гидроагрегата.

2.2. Модель вертикальной вибрации гидроагрегата

Вибрацию гидроагрегата можно описать уравнением вынужденных колебаний массивного тела на упруго-демпферной подвеске (рис.2.2):

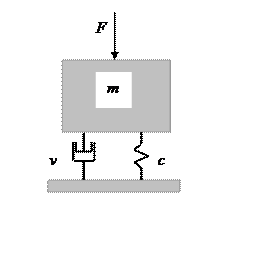
Рис. 2,2. Модель вертикальной вибрации гидроагрегата

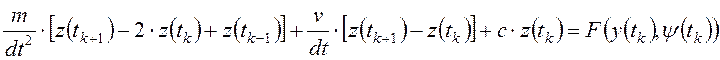,    (2,5)

где:  - масса гидроагрегата;  и  - коэффициенты демпфирования и упругости крепления гидроагрегата к основанию; - равнодействующая возбуждающих сил, зависящая от углов установки лопаток НА и лопастей РК.