Разработка и исследование адаптивной системы управления активной мощностью гидроагрегата ГЭС с поворотно-лопастной турбиной, страница 14

Зависимость равнодействующей возбуждающих сил от углов установки лопаток НА и лопастей РК можно описать с помощью В-сплайнов

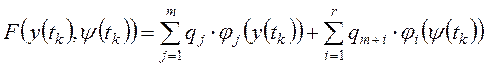.                               (2.6)

С учетом формул (2.6) и (2.3) уравнение (2.5) было преобразовано в следующее уравнение модели вертикальной вибрации гидроагрегата:

,                             (2.7)

где  - возмущающее воздействие, создаваемое неучтенными факторами (погрешность модели вибрации гидроагрегата).

Параметры  модели вибраций (2.7), образующие вектор , определяют с помощью МНК с использованием результатов измерений уровня вертикальной вибрации и углов установки лопаток НА и лопастей РК.

Анализ точности модели (2.7) в разных режимах работы гидроагрегата выполнен в главе 4.

Уравнение (2.7) используется в разделе 2.5 при синтезе обучаемой модели гидроагрегата.

2.3 Математическая модель привода лопастей рабочего колеса и привода лопаток направляющего аппарата турбины

Поворот лопаток НА и лопастей РК турбины осуществляют с помощью следящих электрогидравлических приводов (ЭГП) [59]. Схема ЭГП приведена на рисунке 2.3.

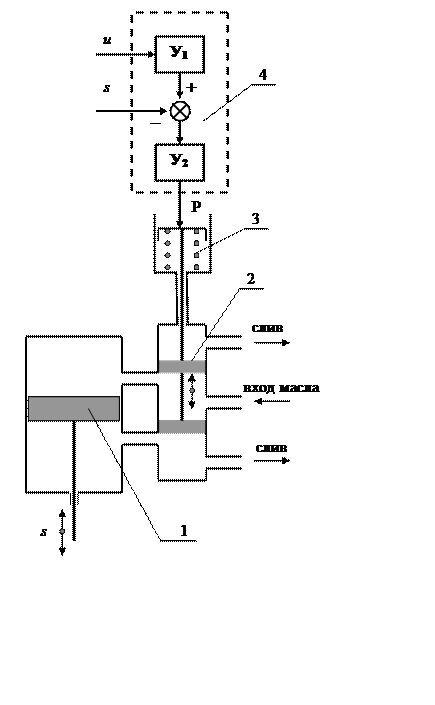
Рис. 2.3. Следящий электрогидравлический привод

1 - поршень сервомотора; 2 - золотник; 3 - пружина; 4 - электронный блок с усилителямиУ₁ и У₂; P - движущая сила электромагнита; s- перемещение штока поршня сервомотора

Перемещением штока поршня 1 сервомотора  ЭГП управляет золотник 2 (рис. 2.3). Шток золотника перемещается в результате совместного действия силы , создаваемой электромагнитом, и силы упругости пружины 3. Движущую силу электромагнита формируют с помощью электронного блока 4 пропорционально сигналу рассогласования между требуемым перемещением поршня сервомотора  (задает регулятор) и его реальным перемещением  (измеряют с помощью датчика и передают в электронный блок по цепи обратной связи).

Динамику рассматриваемых следящих ЭГП описывают с помощью разностных уравнений:

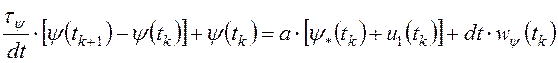;                  (2.8)

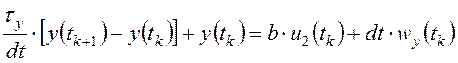,                                    (2.9)

где: ,  - постоянные времени электрогидравлических приводов; ,  - коэффициенты усиления;  - задание электрогидравлическому приводу лопастей РК, сформированное по алгоритму комбинаторной зависимости;  - корректирующее воздействие, создаваемое регулятором;  - задание ЭГП лопаток НА, формируемое регулятором; ,  - возмущающие воздействия, создаваемые неконтролируемыми внутренними и внешними факторами.

Уравнения (2.8) и (2.9) представим в следующем эквивалентном виде:

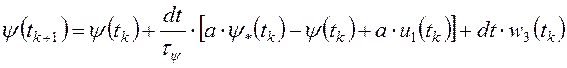;              (2.10)

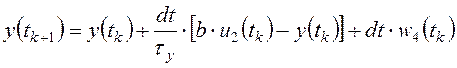,                                 (2.11)

где ,  - возмущающие воздействия неконтролируемых факторов (погрешности модели).

Параметры модели электрогидравлических приводов определяют с помощью метода наименьших квадратов с использованием результатов измерений углов установки лопаток НА и лопастей РК в интервале времени .

Анализ точности модели ЭГП (2.10), (2.11) в разных режимах работы гидроагрегата выполнен в главе 4.

Уравнения (2.10), (2.11) используются в разделе 2.5 при синтезе обучаемой модели гидроагрегата.

2.4 Обучаемая модель гидроагрегата

Синтез и анализ адаптивных систем управления осуществляют с использованием модели объекта управления в виде уравнений модели САУ в пространстве состояний [8]. Поэтому из уравнений  (2.4), (2.7), (2.10), (2.11) получим такую модель гидроагрегата.

Модель процессов, происходящих в гидроагрегате, описывают уравнения  (2.4), (2.7), (2.10), (2.11). А состояние гидроагрегата определяют текущие значения активной мощности, амплитуды вертикальной вибрации и углов установки лопастей РК и лопаток НА турбины. Из этих переменных сформируем вектор переменных состояния гидроагрегата

.                                                  (2.12)

Уравнения (2.4), (2.7), (2.10), (2.11) представим в виде одного матричного уравнения состояния гидроагрегата

,                            (2.13)

где

;   ;

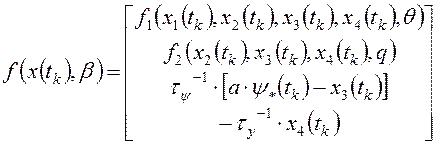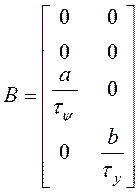 - вектор параметров модели гидроагрегата;  - вектор возмущающих воздействий, создаваемых неконтролируемыми влияющими факторами.