3.1.1 Априорная модель системы управления
![]()
![]() ,
(3.1)
,
(3.1)
где: ![]() - текущее значение выходного сигнала
датчика уровня вертикальной вибрации гидроагрегата;
- текущее значение выходного сигнала
датчика уровня вертикальной вибрации гидроагрегата; ![]() - текущее значение выходного сигнала
датчика положения лопастей РК;
- текущее значение выходного сигнала
датчика положения лопастей РК; ![]() - оценка вектора параметров,
полученная с помощью системы обучения модели гидроагрегата.
- оценка вектора параметров,
полученная с помощью системы обучения модели гидроагрегата.
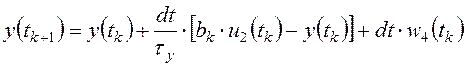 ,
(3.2)
,
(3.2)
где ![]() - оценка коэффициента усиления
электронного блока ЭГП, полученная с помощью системы обучения модели
гидроагрегата;
- оценка коэффициента усиления
электронного блока ЭГП, полученная с помощью системы обучения модели
гидроагрегата; ![]() - управляющее воздействие, формируемое цифровым
регулятором.
- управляющее воздействие, формируемое цифровым
регулятором.
Для уменьшения статической погрешности системы управления в состав регулятора включен интегрирующий блок. Модель такого регулятора описывают в пространстве состояний уравнениями [8]:
![]() ;
(3.3)
;
(3.3)
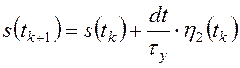 ,
(3.4)
,
(3.4)
Из переменных ![]() ,
,
![]() и
и ![]() составим
вектор переменных состояния системы управления активной мощностью
составим
вектор переменных состояния системы управления активной мощностью
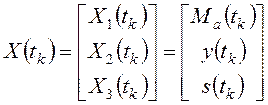 .
(3.5)
.
(3.5)
Тогда уравнения (3.1)-(3.4) можно записать в виде одного матричного уравнения:
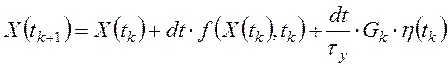 ,
(3.6)
,
(3.6)
 ;
;
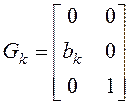 ;
; 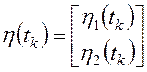 .
.
Переменные состояния гидроагрегата должны находиться внутри области допустимых значений [59]:
![]() ;
(3.7)
;
(3.7)
![]() ;
(3.8)
;
(3.8)
![]() .
(3.9)
.
(3.9)
Границы области допустимых значений задает система группового регулирования активной мощности.
Уравнение (3.6) и неравенства (3.7)-(3.9) задают априорную модель системы управления активной мощностью гидроагрегата. Эта модель используется при синтезе алгоритма управления.
3.1.2 Функционал обобщенной работы в задаче управления
активной мощностью
Для количественной оценки эффективности системы управления введем следующий функционал обобщенной работы:
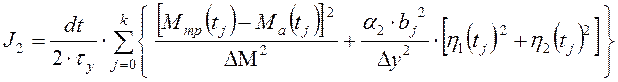 ,
(3.10)
,
(3.10)
где ![]() - допустимая погрешность управления
активной мощностью;
- допустимая погрешность управления
активной мощностью; ![]() - допустимое отклонение угла установки лопаток НА от
требуемых значений, заданных формулами (3.9);
- допустимое отклонение угла установки лопаток НА от
требуемых значений, заданных формулами (3.9); ![]() - весовой коэффициент (параметр
регуляризации).
- весовой коэффициент (параметр
регуляризации).
Первое слагаемое ФОР
(3.10) определяет среднеквадратическую погрешность регулирования активной
мощности. Из уравнений (3.2)-(3.4) следует, что входные сигналы ![]() и
и ![]() регулятора
задают положение лопаток НА, поэтому второе слагаемое ФОР (3.10) определяет
расход воды через турбину.
регулятора
задают положение лопаток НА, поэтому второе слагаемое ФОР (3.10) определяет
расход воды через турбину.
Таким образом, можно
выполнить синтез системы оптимального управления активной мощностью, которая обеспечивает
минимальное отклонение активной мощности генератора ![]() от
требуемых значений
от
требуемых значений ![]() , заданных групповым регулятором
активной мощности, при минимальном расходе воды через турбину.
, заданных групповым регулятором
активной мощности, при минимальном расходе воды через турбину.
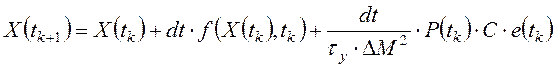 ; (3.12)
; (3.12)Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.