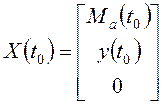 ;
;
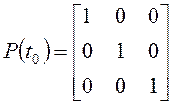 , (3.14)
, (3.14)где ![]() -сигнал рассогласования (динамическая погрешность
регулирования активной мощности)
-сигнал рассогласования (динамическая погрешность
регулирования активной мощности)
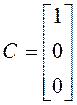 ;
; 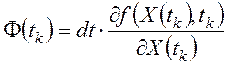 ;
; 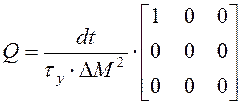 ;
(3.16)
;
(3.16)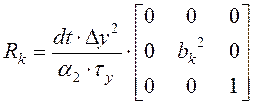 .
(3.17)
.
(3.17)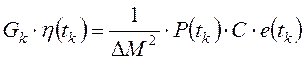 .
.
Поэтому
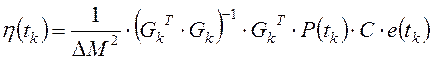 .
(3.18)
.
(3.18)
После выполнения матричных операций в правой части уравнения (3.18) и подстановки результатов вычислений в формулы (3.3), (3.4) был получен алгоритм формирования входного сигнала следящего электрогидравлического привода лопаток НА турбины:
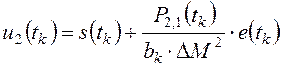 ;
(3.19)
;
(3.19)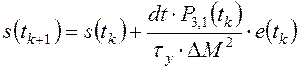 ;
; ![]()
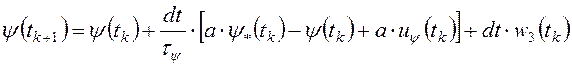
![]()
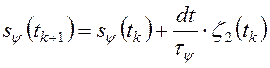
3.1.2 Функционал обобщенной работы в задаче управления
активной мощностью
Для количественной оценки эффективности коррекции введем следующий функционал обобщенной работы:
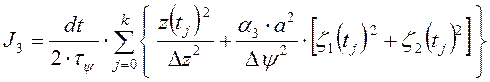 , (3.14)
, (3.14)
где
Анализ точности был выполнен путем сравнения выходного сигнала модели (2.4) с результатами измерений активной мощности гидроагрегата № 8 Волжской ГЭС в разных режимах работы. Результаты анализа приведены на рисунках 2.2 -2.4.
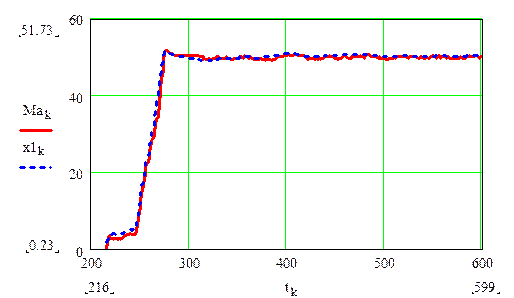
Рис. 2.2. Результаты определения активной мощности гидроагрегата №8 Волжской ГЭС (МВт): результаты измерений - сплошная линия; оценка активной мощности, определенная с помощью модели (2.4) - штриховая линия
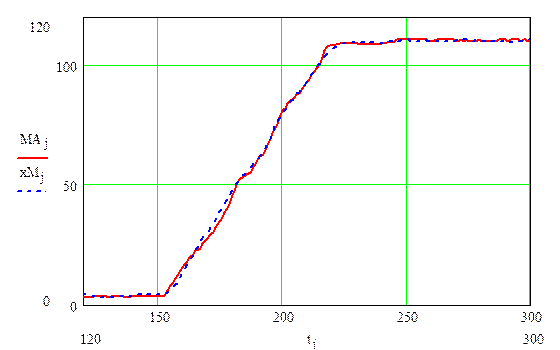
Рис. 2.3. Результаты определения активной мощности гидроагрегата №8 Волжской ГЭС (МВт): результаты измерений - сплошная линия; оценка активной мощности, определенная с помощью модели (2.4) - штриховая линия
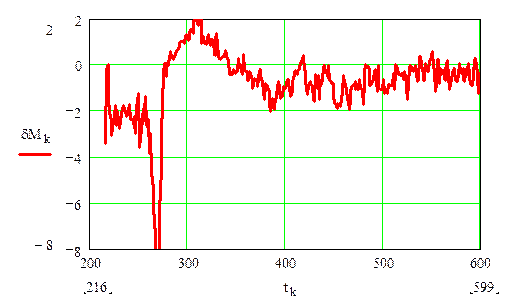
Рис. 2.4. Относительная погрешность определения активной мощности гидроагрегата №8 Волжской ГЭС (%)
В результате такого сравнения было установлено, что модель (2.4) формирует текущие значения активной мощности с погрешностью не более ±8% в переходном режиме и не более ±2% в установившемся режиме.
С помощью алгоритмов оценивания были определены оценки параметров и возмущающего воздействия модели ОУ для агрегатов № 4, № 8 и № 19 при пусках с разными значениями напора воды. Оказалось, что эти величины имеют разные значения для разных гидроагрегатов, существенно изменяются от пуска к пуску и могут изменяться в течение одного пуска каждого гидроагрегата.
С помощью РМНК были определены оценки параметров и возмущающего воздействия модели привода лопастей РК. Оказалось, что эти величины имеют разные значения для разных гидроагрегатов, существенно изменяются от пуска к пуску и могут изменяться в течение одного пуска каждого гидроагрегата (рисунок Ошибка! Ошибка связи.).
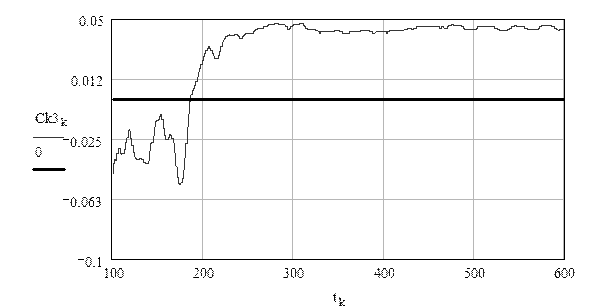
Рисунок 2 – Изменение оценки параметров обучающего воздействаия
Результат обучения модели привода лопастей РК для ГА №8 приведены на рисунках Ошибка! Ошибка связи. и Ошибка! Ошибка связи..
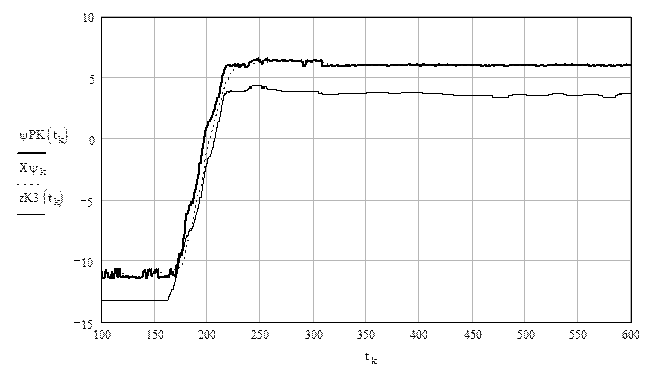 |
Рисунок 3 – результат обучения модели привода лопастей РК
ψРК(t) – угол разворота лопастей РК по модели;
Xψ – угол разворота лопастей РК действующей САУ;
zK3(t) – угол разворота лопастей РК по комбинаторной зависимости.
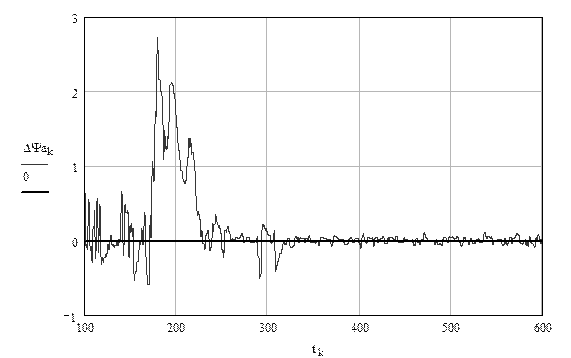
Рисунок 4 - погрешность алгоритма обучения модели привода лопастей РК
На рисунке Ошибка! Ошибка связи. приняты следующие обозначения:
tj – время с момента пуска (с);
ΔΨаk - погрешность алгоритма обучения модели привода лопастей РК (град).
Максимальная погрешность обучения модели составляет 2,78 град. Но в процессе обучения она значительно уменьшается.
1 Среднее квадратичное отклонение погрешности модели привада лопастей РК (град).
|
|
(0.1) |
2 Статическая погрешность предварительно обученной модели
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.