|
|
(2.4.17) |
Таким образом, получена априорная модель объекта управления, в котором происходят процессы с неизвестным математическим описанием, в виде нелинейной динамической системы (2.4.11)-(2.4.17).
ПИ-наблюдатель переменных состояния. Выполним синтез наблюдателя переменных состояния динамической системы (2.4.11)-(2.4.17), оптимального по критерию обобщенного МНК с функцией стоимости
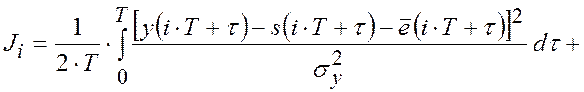
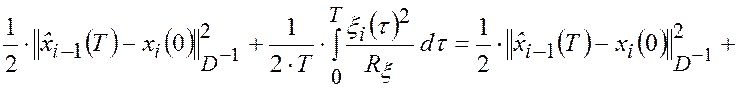
|
|
(2.4.18) |
Оценка ![]() вектора переменных состояния
вектора переменных состояния ![]() , обращающая в минимум функцию стоимости (2.4.18),
обеспечивает минимальную выборочную дисперсию погрешности оценивания
, обращающая в минимум функцию стоимости (2.4.18),
обеспечивает минимальную выборочную дисперсию погрешности оценивания ![]() выходного
сигнала измерительного устройства. Оценку выборочной дисперсии вычисляют усреднением
по времени реализации погрешности оценивания
выходного
сигнала измерительного устройства. Оценку выборочной дисперсии вычисляют усреднением
по времени реализации погрешности оценивания ![]() , полученной во временном окне с номером
, полученной во временном окне с номером ![]() .
.
Из формул (2.4.11)-(2.4.18) следует, что рассматриваемая задача является частным случаем задачи синтеза ПИ‑наблюдателя переменных состояния, которая была рассмотрена в разделе 2.3.1.
После внесения изменений, обусловленных особенностями динамической системы (2.4.11)-(2.4.17), уравнения (2.3.8)-(2.3.13) можно преобразовать в следующие уравнения ПИ‑наблюдателя переменных состояния:
|
|
(2.4.19) |
|
|
(2.4.20) |
|
|
(2.4.21) |
с начальными условиями
|
|
(2.4.22) |
где
|
|
(2.4.23) |
|
|
(2.4.24) |
|
|
(2.4.25) |
Уравнения (2.4.19)–(2.4.25), (2.4.15)-(2.4.17) определяют нели-нейный ПИ‑наблюдатель переменных состояния объекта управления с неизвестным математическим описанием.
Из формул (2.4.24) видно, что матрицы ![]() и
и ![]() положительно полуопределенные, поэтому решение
уравнения Риккати (2.4.21) асимптотически устойчиво при любых погрешностях
задания начальных условий (2.4.22).
положительно полуопределенные, поэтому решение
уравнения Риккати (2.4.21) асимптотически устойчиво при любых погрешностях
задания начальных условий (2.4.22).
При формировании оценок переменных состояния ПИ‑наблю-датель (2.4.19)–(2.4.25), (2.4.15)-(2.4.17) использует в каждом временном окне:
- результаты
измерений выходного сигнала объекта управления ![]() ;
;
- погрешность
оценивания ![]() выходного сигнала измерительного устройства;
выходного сигнала измерительного устройства;
- оценку ![]() среднего значения погрешности оценивания
выходного сигнала измерительного устройства
среднего значения погрешности оценивания
выходного сигнала измерительного устройства ![]() , вычисленную
усреднением по времени в скользящем временном окне;
, вычисленную
усреднением по времени в скользящем временном окне;
- оценку ![]() дисперсии
дисперсии ![]() погрешности
используемой сплайн-аппроксимации (2.4.3).
погрешности
используемой сплайн-аппроксимации (2.4.3).
Пример 2. Сравнительный
анализ наблюдателей перемен-ных состояния сети передачи данных. Сеть передачи
данных (СПД) состоит из отправителя сообщения О, получателя сообщений П и узлов
![]() ,
, ![]() , … ,
, … , ![]() , соединенных между собой линиями связи
(ЛС). Кроме того, на входы узлов
, соединенных между собой линиями связи
(ЛС). Кроме того, на входы узлов ![]() поступают сообщения
поступают сообщения ![]() , переданные получателю П от других
абонентов сети. На рисунке 2.10 изображена сеть передачи данных, содержащая
(помимо отправителя и получателя) три узла и семь линий связи.
, переданные получателю П от других
абонентов сети. На рисунке 2.10 изображена сеть передачи данных, содержащая
(помимо отправителя и получателя) три узла и семь линий связи.
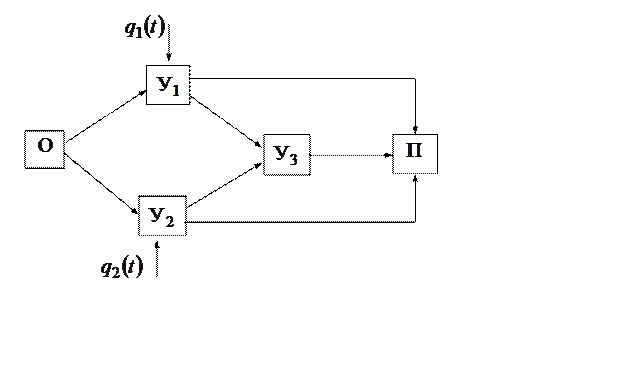
Рис. 2.10. Сеть передачи данных
Как правило, математические модели линий связи СПД не известны. Поэтому системы управления сетями передачи данных содержат подсистемы оценивания переменных состояния линий связи СПД.
В рассматриваемом примере с помощью имитационного моделирования выполнен сравнительный анализ эффективности четырех альтернативных наблюдателей переменных состояния одной и той же линии связи двух узлов СПД. Сравнивались между собой наблюдатель переменных состояния, реализующий алгоритм фильтра Калмана; наблюдатель переменных состояния, реализующий алгоритм рекуррентного МНК; ПИД-наблюдатель (2.3.24)-(2.3.27) и ПИ-наблюдатель (2.4.19)–(2.4.25), в котором применялись В-сплайны первого порядка.
Линия связи двух соседних узлов этой сети передачи данных имеет следующую математическую модель:
|
|
|
|
(2.4.26) |
|
|
(2.4.27) |
|
|
где ![]() - выходной сигнал линии связи (интенсивность
потока ин-формации на выходе из ЛС);
- выходной сигнал линии связи (интенсивность
потока ин-формации на выходе из ЛС); ![]() - входной сигнал ЛС (интен-сивность
потока информации, поступающей на вход ЛС);
- входной сигнал ЛС (интен-сивность
потока информации, поступающей на вход ЛС); ![]() - чув-ствительность скорости
выходного сигнала
- чув-ствительность скорости
выходного сигнала ![]() к изменению входного сигнала
к изменению входного сигнала ![]() линии связи;
линии связи; ![]() - выходной сигнал измери-тельного
устройства;
- выходной сигнал измери-тельного
устройства; ![]() -
параметр, имеющий размерность времени;
-
параметр, имеющий размерность времени; ![]() - шум линии связи;
- шум линии связи; ![]() -
погрешность измерений.
-
погрешность измерений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.