Таким образом, получена априорная модель системы управления в виде системы нелинейных дифференциальных и алгебраических уравнений для генератора возмущающих воздействий (2.1.4), (2.1.8) - (2.1.11); генератора допустимых управляющих воздействий (2.1.13) - (2.1.15), объекта управления (2.1.16), (2.1.17) и измерительных устройств (2.1.20), (2.1.21) (или (2.1.25)-(2.1.27)).
Генератор возмущающих воздействий (2.1.4), (2.1.8)-(2.1.11) формирует в скользящем временном окне возмущающие воздействия
в виде непрерывных функций времени ![]() из белых шумов
из белых шумов ![]() с нулевыми средними значениями. В общем
случае функции распреде-ления вероятности белых шумов
с нулевыми средними значениями. В общем
случае функции распреде-ления вероятности белых шумов ![]() неизвестны.
неизвестны.
Допустимые управляющие воздействия формируют в виде непрерывных функций
времени из вспомогательных функций ![]() с помощью линейной
динамической системы (2.1.14), (2.1.15) и нелинейного преобразователя (2.1.13).
с помощью линейной
динамической системы (2.1.14), (2.1.15) и нелинейного преобразователя (2.1.13).
Модель измерительных устройств содержит белые шумы ![]() с нулевыми средними значениями и
известными интенсивностями. В общем случае функции распределения вероятности
белых шумов
с нулевыми средними значениями и
известными интенсивностями. В общем случае функции распределения вероятности
белых шумов ![]() неизвестны.
неизвестны.
Важной особенностью полученной априорной модели системы управления
является то, что в уравнения этой модели входят линейно неизвестные белые шумы ![]() ,
, ![]() и
и ![]() . В следующей главе будет показано, что для
синтеза оптимальной системы управления следует применять квадратичные критерии
качества. Поэтому такая система управления является нейтральной и можно
применять теорему разделения [20], [29]. Другой важной особенностью этой модели
является то, что уравнения наблюдения (2.1.20), (2.1.21), (2.1.25)-(2.1.27) учитывают средние значения погрешностей измере-ний выходных
сигналов объекта управления. Это позволяет осуществить синтез наблюдателей
переменных состояния, которые могут формировать состоятельные несмещенные
оценки переменных состояния объекта управления.
. В следующей главе будет показано, что для
синтеза оптимальной системы управления следует применять квадратичные критерии
качества. Поэтому такая система управления является нейтральной и можно
применять теорему разделения [20], [29]. Другой важной особенностью этой модели
является то, что уравнения наблюдения (2.1.20), (2.1.21), (2.1.25)-(2.1.27) учитывают средние значения погрешностей измере-ний выходных
сигналов объекта управления. Это позволяет осуществить синтез наблюдателей
переменных состояния, которые могут формировать состоятельные несмещенные
оценки переменных состояния объекта управления.
2.2. Критерии синтеза наблюдателей переменных состояния
Синтез наблюдателей переменных состояния осуществляют по результатам измерений управляющих воздействий и выходных сигналов измерительных устройств.
В зависимости от имеющейся априорной информации о функциях распределения погрешностей измерений и погрешностей аппроксимации возмущающих воздействий, например, В-сплайнами можно сформировать разные критерии оценивания переменных состояния объекта управления.
2.2.1. Критерии максимума апостериорной вероятности
в системах с гауссовскими шумами
Если погрешности измерений и погрешности аппроксимации возмущающих воздействий В-сплайнами являются гауссовскими случайными процессами, то задачу синтеза наблюдателя переменных состояния можно сформулировать как задачу оптимального оценивания по критерию максимума апостериорной вероятности (по критерию МАВ).
Системы с белыми шумами. В частности, часто погрешности измерений ![]() и погрешности аппроксимации
и погрешности аппроксимации ![]() можно считать белыми шумами с гауссовскими
плотностями распределения вероят-ности, нулевыми средними значениями и
матрицами интенсивностей
можно считать белыми шумами с гауссовскими
плотностями распределения вероят-ности, нулевыми средними значениями и
матрицами интенсивностей ![]() и
и ![]() соответственно.
соответственно.
Для составления критерия МАВ сформируем вектор
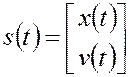 .
.
Тогда априорную математическую модель объекта управления (2.1.4), (2.1.8)-(2.1.11), (2.1.16), (2.1.17) можно представить в следующем эквивалентном виде
|
|
(2.2.1) |
|
|
(2.2.2) |
|
|
(2.2.3) |
где вектор ![]() составлен из выходных
сигналов измерительных устройств по формуле (2.1.21).
составлен из выходных
сигналов измерительных устройств по формуле (2.1.21).
При известном управляющем воздействии ![]() оптимальная оценка
оптимальная оценка ![]() вектора
переменных состояния
вектора
переменных состояния ![]() (оценка, оптимальная по критерию
МАВ) обращает в максимум условную плотность
(оценка, оптимальная по критерию
МАВ) обращает в максимум условную плотность ![]() на
всем интервале времени
на
всем интервале времени ![]() измерений выходных сигналов
измерений выходных сигналов ![]() измерительных устройств [21], где
измерительных устройств [21], где ![]() - множество
непрерывных реализаций переменных состояния
- множество
непрерывных реализаций переменных состояния ![]() ;
; ![]() - множество
непрерывных реализаций выходных сигналов измерительных устройств
- множество
непрерывных реализаций выходных сигналов измерительных устройств ![]() на этом интервале времени.
на этом интервале времени.
По формуле Байеса
|
|
(2.2.4) |
Так как вектор ![]() составлен
из случайных гауссовских величин с известными вероятностными характеристиками,
а
составлен
из случайных гауссовских величин с известными вероятностными характеристиками,
а ![]() и
и ![]() - векторы случайных гауссовских процессов, то условная плотность
- векторы случайных гауссовских процессов, то условная плотность ![]() является гауссовской. При этом из (2.2.3)
следует, что
является гауссовской. При этом из (2.2.3)
следует, что
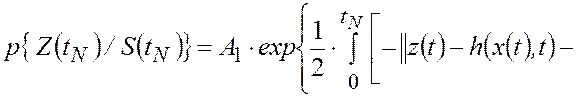
|
|
(2.2.5) |
где ![]() - параметр, величина которого не зависит от переменных
- параметр, величина которого не зависит от переменных ![]() ,
, ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.