Синтез оптимальных наблюдателей переменных состояния нелинейных объектов управления, страница 10

Был рассмотрен случай, когда шум линии связи  и погрешность измерений  являются случайными процессами с нулевыми средними значениями и ковариационными функциями, приведенными на рисунках 2.11 и 2.12.

Моделирование осуществлялось в относительном времени . В наблюдателе переменных состояния, реализующем алгоритм фильтра Калмана, переменная  была известна, случайный процесс  - цветной шум с ковариационной функцией, вычисленной по формуле (2.1.22), а погрешность измерений  считали белым шумом с нулевым средним значением  и интенсивностью .

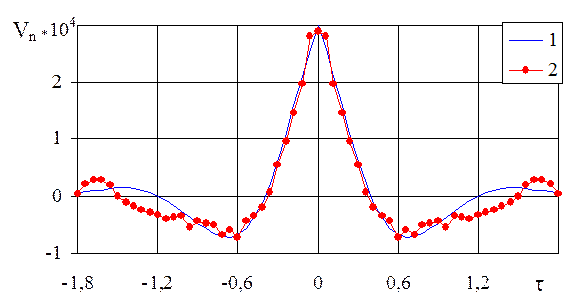
Рис. 2.11. Ковариационная функция погрешности измерений:

1 – значения ковариационной функции, вычисленные по формуле (2.1.28);

 2 – действительные значения ковариационной функции

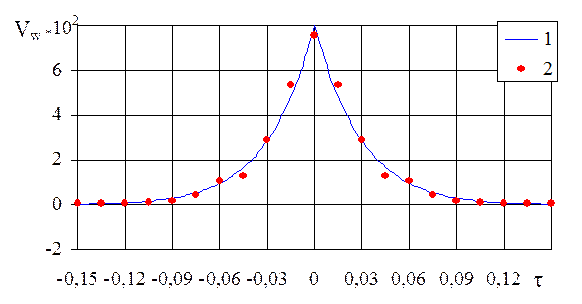
Рис. 2.12. Ковариационная функция случайного процесса :

1– значения ковариационной функции, вычисленные по формуле (2.1.22);

 2 – действительные значения ковариационной функции

В ПИД-наблюдателе (2.3.24)-(2.3.27)  переменная  была известна, а случайные процессы  и  считали цветными шумами с автоковариационными функциями, вычисленными по формуле (2.1.22).

В ПИ-наблюдателе (2.4.19)–(2.4.25) предполагается, что переменная  - неизвестная функция времени,  - цветной шум с ковариационной функцией (2.1.22), а  - белый шум с неизвестным средним значением и интенсивностью .

В рекуррентном МНК  переменная  была известна и предполагалось, что , а  - белый шум с интенсивностью .

Графики изменения переменных  и  во времени , построенные с использованием формул (2.4.26) и (2.1.27), изображены на рисунках 2.13 и 2.14.

Моделирование процессов оценивания переменных состояния линии связи выполнялось при разных реализациях случайных процессов  и .

Результаты оценивания переменных состояния при реализации одного из этих вариантов приведены на рисунках 2.15 и 2.16.

На рисунке 2.15 изображены относительные погрешности оценивания переменной состояния .

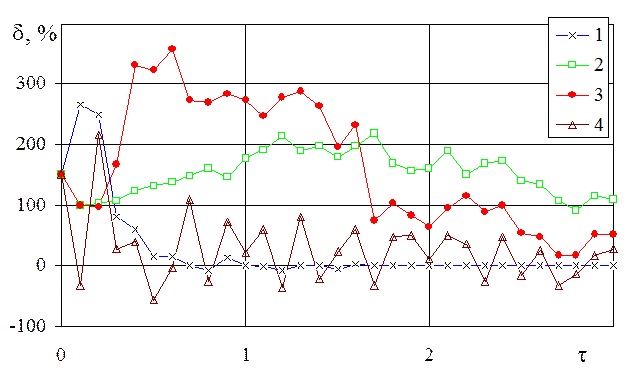
Рис. 2.15. Относительная погрешность оценивания

переменной состояния :

1 – с помощью ПИ-наблюдателя (2.4.19)–(2.4.25); 2 – по уравнениям фильтра Калмана;  3 – с помощью рекуррентного МНК; 4 – по алгоритму ПИД‑наблюдателя (2.3.24)-(2.3.27)

На рисунке 2.16 изображены результаты оценивания с помощью ПИ-наблюдателя (2.4.19)–(2.4.25) дисперсии  шума .

Результаты имитационного моделирования показали, что все четыре метода формируют состоятельные оценки. При времени наблюдения выходного сигнала измерительного устройства  все четыре метода имеют погрешность оценивания переменной состояния  меньше 1 %. Но лучшие показатели по скорости схо-димости и точности обеспечивает ПИ-наблюдатель (2.4.19)–(2.4.25). ПИ-наблюдатель (2.4.19)–(2.4.25) обеспечивает погрешность оцени-вания этой переменной состояния меньше 1 % при использовании результатов измерений, выполненных за время . ПИД-наблюдатель переменных состояния имеет высокую чувствительность к случайным погрешностям измерений , так как в нем исполь-зуются производные по времени от выходного сигнала измеритель-ного устройства.

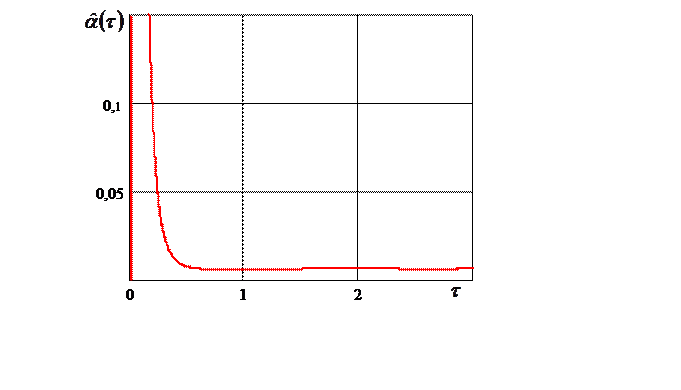
Рис. 2.16. График изменения во времени оценки

нормированной дисперсии шума линии связи

Аналогичные результаты были получены и при других реализациях случайных процессов  и .

Таким образом, разработан алгоритм оценивания переменных состояния объекта с неизвестной математической моделью происходящих в нем процессов. ПИ-наблюдатель переменных состояния, который реализует этот алгоритм, обеспечивает несмещен-ные состоятельные оценки переменных состояния этого объекта с минимальной дисперсией погрешности оценивания выходного сигнала измерительного устройства.

В разделе 3.4 ПИ-наблюдатель (2.4.19)–(2.4.25) используется при синтезе адаптивной системы автоматического управления объектом с неизвестным математическим описанием происходящих в нем процессов.

2.5. Выводы

В главе 2 рассмотрена задача синтеза наблюдателя переменных состояния нелинейного динамического объекта (2.1.16)-(2.1.18) с ограничениями (2.1.1), (2.1.11) и произвольными функциями распределения случайных возмущающих воздействий и погреш-ностей измерений.