Так как ![]() - вектор белых
шумов с гауссовскими плотностями распределения вероятности, а вектор
- вектор белых
шумов с гауссовскими плотностями распределения вероятности, а вектор ![]() составлен из случайных гауссовских величин
то из (2.2.1), (2.2.2), (2.1.8) и (2.1.11) следует, что
составлен из случайных гауссовских величин
то из (2.2.1), (2.2.2), (2.1.8) и (2.1.11) следует, что
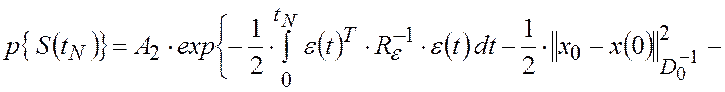
|
|
(2.2.6) |
где ![]() - параметр, величина которого не зависит от переменных
- параметр, величина которого не зависит от переменных ![]() ,
, ![]() и
и ![]() .
.
Плотность распределения вероятности ![]() не
зависит от переменных
не
зависит от переменных ![]() ,
, ![]() и
и ![]() . Поэтому формулу (2.2.4) после подстановки
выражений (2.2.5) и (2.2.6) можно представить в следующем виде:
. Поэтому формулу (2.2.4) после подстановки
выражений (2.2.5) и (2.2.6) можно представить в следующем виде:
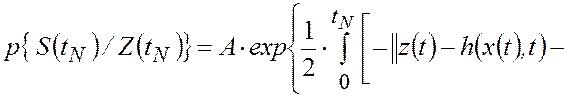
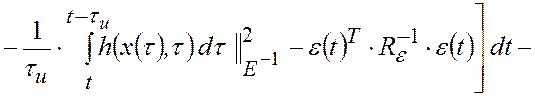
|
|
(2.2.7) |
Таким образом, наблюдатель переменных состояния дина-мической системы (2.2.1)-(2.2.3), оптимальный по критерию МАВ, должен формировать оценки
переменных состояния путем оптимизации функционала (2.2.7) по переменным ![]() ,
, ![]() и
и ![]() при ограничениях (2.2.1), (2.1.4),
(2.1.21).
при ограничениях (2.2.1), (2.1.4),
(2.1.21).
Системы с цветными шумами. В другом частном
случае состояние объекта управления вновь описывают уравнениями (2.1.16), но
теперь погрешности измерений ![]() и погрешности аппроксимации
и погрешности аппроксимации
![]() являются гауссовскими цветными шумами с
корреляционными функциями (2.1.22) и (2.1.5). При этом начальные условия (2.1.10)
и (2.1.17) являются гауссовскими случайными величинами.
являются гауссовскими цветными шумами с
корреляционными функциями (2.1.22) и (2.1.5). При этом начальные условия (2.1.10)
и (2.1.17) являются гауссовскими случайными величинами.
Для составления критерия максимума апостериорной вероятности сформируем векторы
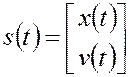 ,
,
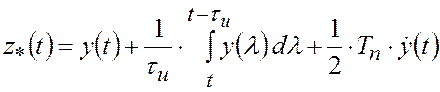 .
.
Тогда априорную математическую модель объекта управления можно описать дифференциальными уравнениями (2.2.1) с начальными условиями (2.2.2) и уравнением (2.1.25).
В этих уравнениях ![]() и
и ![]() –
векторы белых шумов, которые имеют гауссовские распределения вероятности,
нулевые средние значения и матрицы интенсивностей (2.1.8) и (2.1.24). Поэтому
условная плотность
–
векторы белых шумов, которые имеют гауссовские распределения вероятности,
нулевые средние значения и матрицы интенсивностей (2.1.8) и (2.1.24). Поэтому
условная плотность
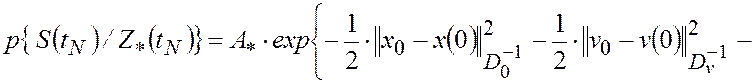
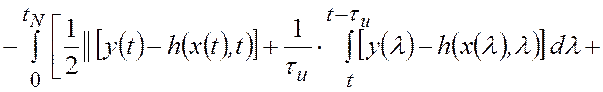
|
|
(2.2.8) |
Из (2.2.8) следует, что в рассматриваемом случае для синтеза
наблюдателя переменных состояния необходимо применять систему измерительных
устройств выходных сигналов объекта управления, выполненную в виде
параллельного соединения пропорционального (П), интегрирующего (И) и
дифференцирующего (Д) звеньев (рис. 2.4). Выходной сигнал такого
соединения содержит погреш-ность измерения в виде белого шума ![]() .
.
Таким образом, наблюдатель переменных состояния системы с гауссовскими
цветными шумами, оптимальный по критерию МАВ, должен формировать оценки
переменных состояния путем оптимизации функционала (2.2.8) по переменным ![]() ,
, ![]() и
и ![]() с учетом ограничений (2.2.1), (2.1.4),
(2.1.27).
с учетом ограничений (2.2.1), (2.1.4),
(2.1.27).
2.2.2. Критерии метода наименьших квадратов
Функция стоимости ПИ-наблюдателя переменных состояния объекта управления с произвольными шумами. В общем случае, когда плотности распределения вероятности погрешностей измерений и (или) возмущающих воздействий не известны, можно сформировать следующую функцию стоимости обобщенного метода наименьших квадратов:
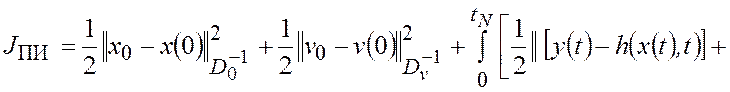
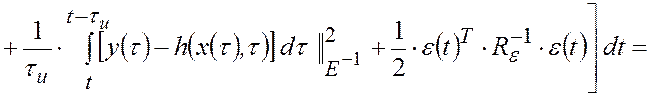
|
|
(2.2.9) |
где ![]() и
и ![]() - матрицы
дисперсий погрешностей задания начальных условий, а
- матрицы
дисперсий погрешностей задания начальных условий, а ![]() и
и ![]() - положительно
определенные матрицы весовых коэффициентов, которые имеют размерность энергии
сигналов
- положительно
определенные матрицы весовых коэффициентов, которые имеют размерность энергии
сигналов ![]() и
и ![]() ;
; ![]() - вектор погрешностей
оценивания выходных сигналов
- вектор погрешностей
оценивания выходных сигналов ![]() измерительных устройств:
измерительных устройств:
|
|
(2.2.10) |
Функция стоимости (2.2.9) составлена аддитивной сверткой частных показателей, определяющих:
- квадраты погрешностей задания начальных условий (первые два слагаемых функции стоимости (2.2.9));
- средние
квадраты отклонений погрешностей оценивания выходных сигналов измерительных
устройств ![]() от своих средних значений
от своих средних значений ![]() , вычисленных усреднением по времени в
скользящем временном окне (2.2.10) (выборочные оценки дисперсий погреш-ностей
оценивания);
, вычисленных усреднением по времени в
скользящем временном окне (2.2.10) (выборочные оценки дисперсий погреш-ностей
оценивания);
- средние
квадраты погрешностей аппроксимации ![]() возмущающих воздействий
(последнее слагаемое функции стои-мости (2.2.9)).
возмущающих воздействий
(последнее слагаемое функции стои-мости (2.2.9)).
Из формул (2.2.9), (2.2.7), (2.1.21) видно, что если
вектор погрешностей аппроксимации ![]() и векторы погрешностей
измерений
и векторы погрешностей
измерений ![]() и
и ![]() образованы
гауссовскими белыми шумами с нулевыми средними значениями и матрицами
интенсивностей
образованы
гауссовскими белыми шумами с нулевыми средними значениями и матрицами
интенсивностей ![]() ,
, ![]() и
и ![]() , то максимизация условной плотности
, то максимизация условной плотности ![]() эквивалентна минимизации квадратичной
функции стоимости (2.2.9).
эквивалентна минимизации квадратичной
функции стоимости (2.2.9).
Функция стоимости (2.2.9) содержит взвешенную сумму по-грешностей
оценивания ![]() (пропорциональная (П) часть функции
стоимости) и взвешенную сумму средних значений (2.2.10) погреш-ностей
оценивания (интегральная (И) часть функции стоимости). Поэтому выражение (2.2.9)
будем называть функцией стоимости ПИ-наблюдателя обобщенного метода
наименьших квадратов (функцией стоимости МНК) для нелинейного
объекта управления (2.2.1)-(2.2.3), (2.1.4) с произвольными
шумами.
(пропорциональная (П) часть функции
стоимости) и взвешенную сумму средних значений (2.2.10) погреш-ностей
оценивания (интегральная (И) часть функции стоимости). Поэтому выражение (2.2.9)
будем называть функцией стоимости ПИ-наблюдателя обобщенного метода
наименьших квадратов (функцией стоимости МНК) для нелинейного
объекта управления (2.2.1)-(2.2.3), (2.1.4) с произвольными
шумами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.