2.1.4. Математическая модель измерительных устройств
В общем случае выходные сигналы ![]() измерительных
устройств, образующие вектор
измерительных
устройств, образующие вектор ![]() , связаны с переменными
состояния нелинейным уравнением
, связаны с переменными
состояния нелинейным уравнением
|
|
(2.1.18) |
где ![]() – вектор известных
непрерывных функций своих аргументов;
– вектор известных
непрерывных функций своих аргументов; ![]() –
вектор, образованный неизвестными средними значениями погрешностей измерений;
–
вектор, образованный неизвестными средними значениями погрешностей измерений; ![]() - вектор,
образованный случайными составляющими погрешностей измерений
- вектор,
образованный случайными составляющими погрешностей измерений ![]() , которые имеют нулевые средние значения и
известные корреляционные функции.
, которые имеют нулевые средние значения и
известные корреляционные функции.
Корреляционные функции погрешностей измерений ![]() можно
использовать для составления математических моделей измерительных устройств.
можно
использовать для составления математических моделей измерительных устройств.
Модель измерительных устройств с погрешностями
измерений в виде белых шумов. Часто
времена корреляции ![]() погрешностей измерений
погрешностей измерений ![]() являются величинами второго порядка
малости по сравнению со временами корреляции переменных состояния объекта
управления. В этих случаях погрешности измерений
являются величинами второго порядка
малости по сравнению со временами корреляции переменных состояния объекта
управления. В этих случаях погрешности измерений ![]() можно
считать белыми шумами с нулевыми средними значениями и матрицей интенсивностей
можно
считать белыми шумами с нулевыми средними значениями и матрицей интенсивностей ![]() .
.
Для составления математической модели измерительных
устройств необходимо из уравнения (2.1.18) исключить вектор ![]() неизвестных средних значений погрешностей
измерений. Для этого в скользящем временном окне определим средние по времени
значения выходных сигналов измерительных устройств
неизвестных средних значений погрешностей
измерений. Для этого в скользящем временном окне определим средние по времени
значения выходных сигналов измерительных устройств
|
|
(2.1.19) |
Из (2.1.18) и (2.1.19) следует, что
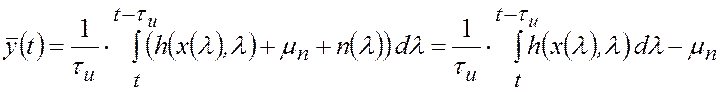 .
.
Поэтому, исключив из (2.1.18) вектор ![]() , получим математическую модель
измерительных устройств с белыми шумами
, получим математическую модель
измерительных устройств с белыми шумами
|
|
(2.1.20) |
|
|
(2.1.21) |
Из формул (2.1.20) и (2.1.21) видно, что вектор ![]() является
выходным сигналом системы, образованной параллельным соединением
пропорционального (первое слагаемое в формуле (2.1.21)) и интегрирующего
(второе слагаемое) звеньев (рис. 2.3).
является
выходным сигналом системы, образованной параллельным соединением
пропорционального (первое слагаемое в формуле (2.1.21)) и интегрирующего
(второе слагаемое) звеньев (рис. 2.3).
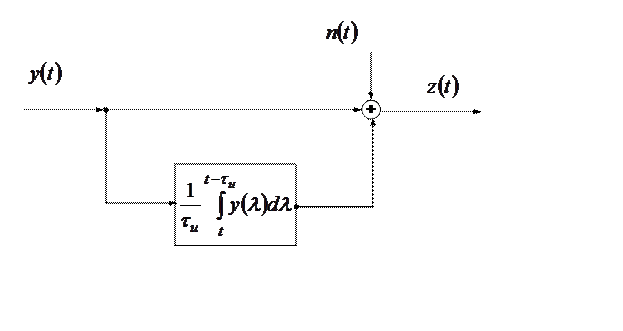
Рис. 2.3. Система измерительных устройств с белыми шумами
Модель измерительных устройств с цветными шумами. В общем случае погрешности измерений ![]() нельзя считать белыми шумами. Поэтому
математическую модель измерительного устрой-ства следует определять с учетом
корреляционной функции погрешностей измерений.
нельзя считать белыми шумами. Поэтому
математическую модель измерительного устрой-ства следует определять с учетом
корреляционной функции погрешностей измерений.
В используемом скользящем временном окне
корреляционную функцию погрешности измерений ![]() с
достаточной точностью можно описать формулой
с
достаточной точностью можно описать формулой
|
|
(2.1.22) |
В разделе 2.1.1 было показано, что корреляционную функцию (2.1.22) имеет случайный процесс, формируемый генератором цветного шума
|
|
(2.1.23) |
где ![]() – белый шум с нулевым
средним значением и интенсивностью
– белый шум с нулевым
средним значением и интенсивностью
|
|
(2.1.24) |
В пределах рассматриваемого временного окна ![]() . Поэтому из уравнений (2.1.23), (2.1.18)-(2.1.21), (2.1.16) и (2.1.4) можно получить, исключая
. Поэтому из уравнений (2.1.23), (2.1.18)-(2.1.21), (2.1.16) и (2.1.4) можно получить, исключая ![]() и
и ![]() ,
следующую математическую модель измерительных устройств:
,
следующую математическую модель измерительных устройств:
|
|
(2.1.25) |
где ![]() – диагональная матрица
времен корреляции погрешностей измерений;
– диагональная матрица
времен корреляции погрешностей измерений; ![]() –
вектор белых шумов с нулевыми средними значениями и интенсивностями (2.1.24);
–
вектор белых шумов с нулевыми средними значениями и интенсивностями (2.1.24);
|
|
(2.1.26) |
|
|
(2.1.27) |
Из (2.1.26) видно, что вектор ![]() составлен
из выходных сигналов системы, образованной параллельным соединением
пропорционального (первое слагаемое в формуле (2.1.26)), интегрирующего (второе
слагаемое) и дифференцирующего (третье слагаемое) звеньев (рис. 2.4).
составлен
из выходных сигналов системы, образованной параллельным соединением
пропорционального (первое слагаемое в формуле (2.1.26)), интегрирующего (второе
слагаемое) и дифференцирующего (третье слагаемое) звеньев (рис. 2.4).
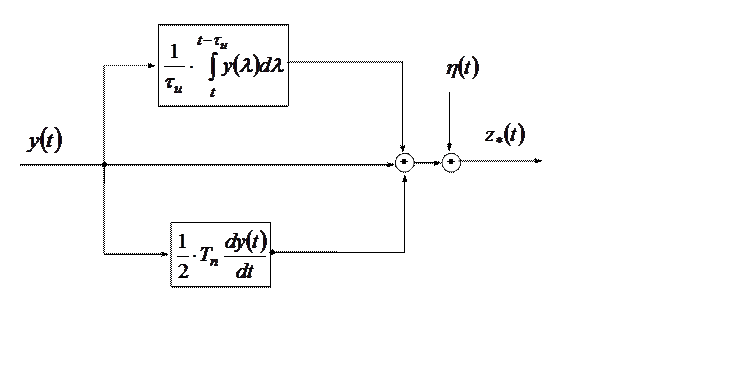
Рис. 2.4. Система измерительных устройств
В некоторых случаях погрешности измерений ![]() имеют
корреляционные функции
имеют
корреляционные функции
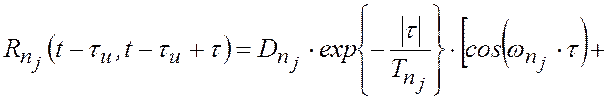
|
|
(2.1.28) |
Аналогичными преобразованиями можно показать, что математическую модель таких измерительных устройств можно описать уравнениями
|
|
(2.1.29) |
|
|
(2.1.30) |
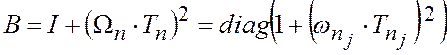 ,
,
где ![]() – вектор белых шумов с
нулевыми средними значениями и матрицей интенсивностей
– вектор белых шумов с
нулевыми средними значениями и матрицей интенсивностей ![]() .
Следовательно, в зависимости от имеющейся априорной информации о корреляцион-ных
функциях погрешностей измерений можно составить различные математические модели
измерительных систем с эквивалентными белыми шумами.
.
Следовательно, в зависимости от имеющейся априорной информации о корреляцион-ных
функциях погрешностей измерений можно составить различные математические модели
измерительных систем с эквивалентными белыми шумами.
Обычно измерительные устройства проектируют так, чтобы погрешности измерений имели быстро убывающие корреляционные функции [56]. Поэтому в дальнейшем ограничимся математическими моделями измерительных устройств (2.1.20), (2.1.21) и (2.1.25)-(2.1.27).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.