Задачасинтеза адаптивной системы автоматического управления объектом с неизвестной математической моделью рассматривалась А. А. Красовским [9]. Он разработал пропор-циональный самоорганизующийся регулятор, который формирует управляющее воздействие, обращающее в минимум функционал обобщенной работы.
Для уменьшения статической погрешности управления, присущей всем пропорциональным регуляторам, в регуляторе Красовского все время регулирования разбивают на отдельные временные окна (циклы) и используют несколько альтернативных моделей объекта управления. В каждом окне регулятор формирует с использованием каждой модели свой вариант управляющего воздействия. Из этого множества альтернативных управляющих воздействий выбирают простым перебором вариант, который обеспечивает минимальное значение используемой функции стоимости.
Этот недостаток можно устранить, если в системе автоматического управления применять наблюдатель переменных состояния, разработанный в разделе 2.3.
Априорная модель объекта управления. Рассматривается задача синтеза математической модели
объекта управления, который имеет выходной сигнал ![]() ,
доступный измерениям, и управляющее воздействие
,
доступный измерениям, и управляющее воздействие ![]() . Кроме
того, на этот объект действуют неизвестные возмущающие воздействия. Структура
объекта и физическая модель происходящих в нем процессов неизвестны.
Математическая модель объекта предназначается для использования в адаптивной
системе автоматического управления этим объектом.
. Кроме
того, на этот объект действуют неизвестные возмущающие воздействия. Структура
объекта и физическая модель происходящих в нем процессов неизвестны.
Математическая модель объекта предназначается для использования в адаптивной
системе автоматического управления этим объектом.
Для составления априорной модели объекта управления весь промежуток
времени ![]() , в котором осуществляют управление этим
объектом, разобьем на отдельные интервалы (окна) протяженностью
, в котором осуществляют управление этим
объектом, разобьем на отдельные интервалы (окна) протяженностью ![]() . Тогда в пределах окна с номером
. Тогда в пределах окна с номером ![]() , где
, где ![]() ,
, ![]() , можно составить следующую модель динамики
объекта управления:
, можно составить следующую модель динамики
объекта управления:
|
|
(2.4.1) |
|
|
(2.4.2) |
где ![]() ,
, ![]() и
и ![]() - неизвестные функции времени.
- неизвестные функции времени.
Изменение во времени переменных ![]() ,
, ![]() и
и ![]() можно
аппроксимировать, например, В-сплайнами [55]:
можно
аппроксимировать, например, В-сплайнами [55]:
![]() ,
,
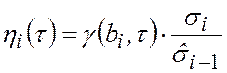 ,
,
|
|
(2.4.3) |
где ![]() ,
, ![]() ,
, ![]() - известные
финитные функции, вид которых зависит от порядка сплайнов;
- известные
финитные функции, вид которых зависит от порядка сплайнов; ![]() ,
, ![]() ,
, ![]() - векторы неиз-вестных параметров (коэффициентов
В-сплайнов);
- векторы неиз-вестных параметров (коэффициентов
В-сплайнов); ![]() - средне-квадратическое
отклонение суммарной погрешности аппроксимации;
- средне-квадратическое
отклонение суммарной погрешности аппроксимации; ![]() - известная оценка среднеквадратического
отклонения погреш-ности аппроксимации в окне с номером
- известная оценка среднеквадратического
отклонения погреш-ности аппроксимации в окне с номером ![]() ;
;
![]() - нормированная погрешность аппроксимации (случайный
процесс с интенсивностью
- нормированная погрешность аппроксимации (случайный
процесс с интенсивностью ![]() ).
).
Выходной сигнал измерительного устройства ![]() связан с выходным сигналом объекта
связан с выходным сигналом объекта ![]() уравнением
уравнением
|
|
(2.4.4) |
где ![]() – среднее значение погрешности
прогноза выходного сигнала измерительного устройства;
– среднее значение погрешности
прогноза выходного сигнала измерительного устройства; ![]() –
случайная составляющая погреш-ности измерений, которая имеет нулевое среднее
значение и дисперсию
–
случайная составляющая погреш-ности измерений, которая имеет нулевое среднее
значение и дисперсию ![]() .
.
В скользящем временном окне, которое имеет величину ![]() , вычислим оценку среднего значения
погрешности оценивания выходного сигнала измерительного устройства по формуле
, вычислим оценку среднего значения
погрешности оценивания выходного сигнала измерительного устройства по формуле
|
|
(2.4.5) |
Выполним дифференцирование правых и левых частей равенства (2.4.4) по
переменной ![]() и исключим из полученных выражений
переменную
и исключим из полученных выражений
переменную ![]() , используя уравнение (2.4.5) и равенство
, используя уравнение (2.4.5) и равенство ![]() . В результате получим модель
измерительного устройства
. В результате получим модель
измерительного устройства
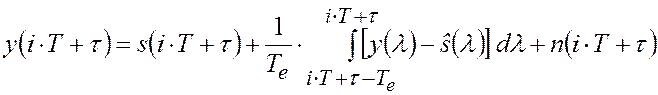 ,
,
которую можно представить в следующем эквивалентном виде:
|
|
(2.4.6) |
где ![]() - решение дифференциального уравнения
- решение дифференциального уравнения
|
|
(2.4.7) |
с начальными условиями
|
|
(2.4.8) |
![]() - погрешность оценивания выходного сигнала измеритель-ного устройства
- погрешность оценивания выходного сигнала измеритель-ного устройства
|
|
(2.4.9) |
Таким образом, в используемом временном окне с номером ![]() состояние объекта управления определяют
переменные
состояние объекта управления определяют
переменные ![]() ,
, ![]() и параметры
и параметры
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Для
оценивания неизвестной дисперсии
. Для
оценивания неизвестной дисперсии ![]() совместно с другими
переменными воспользуемся преобразованием модели объекта управления,
предложенным в [59]. Для этого составим вектор переменных состояния объекта:
совместно с другими
переменными воспользуемся преобразованием модели объекта управления,
предложенным в [59]. Для этого составим вектор переменных состояния объекта:
|
|
(2.4.10) |
Тогда в матричной форме записи уравнения (2.4.1), (2.4.3), (2.4.6) и (2.4.7) примут следующий вид:
|
|
(2.4.11) |
|
|
(2.4.12) |
|
|
(2.4.13) |
|
|
(2.4.14) |
|
|
(2.4.15) |
|
|
(2.4.16) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.