В разделе 2.2 для рассматриваемой в теореме 1 задачи оценивания получена функция стоимости (2.2.7) критерия МАВ. Очевидно, что максимизация условной плотности (2.2.7) при ограничениях (2.2.1), (2.1.4), (2.1.21) эквивалентна минимизации квадратичной функции стоимости (2.2.9) при ограничениях (2.2.1), (2.1.4), (2.1.21), (2.3.15).
Для решения этой вариационной задачи применим метод неопределенных множителей Лагранжа. Функция Гамильтона рассматриваемой задачи
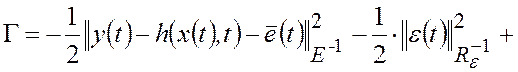
![]()
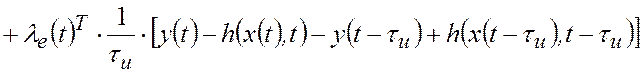 ,
,
где ![]() ,
, ![]() и
и ![]() - множители Лагранжа. Оптимальное решение удовлетворяет следующим
уравнениям Эйлера-Лагранжа:
- множители Лагранжа. Оптимальное решение удовлетворяет следующим
уравнениям Эйлера-Лагранжа:
![]() ,
,
|
|
(2.3.16) |
|
|
(2.3.17) |
|
|
(2.3.18) |
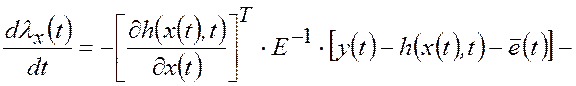
|
|
(2.3.19) |
|
|
(2.3.20) |
|
|
(2.3.21) |
с краевыми условиями
|
|
|
|
(2.3.22) |
|
|
(2.3.23) |
Выполним инвариантное погружение двухточечной краевой задачи (2.2.16)-(2.2.23). С помощью инвариантного погружения [57]-[59] двухточечная краевая задача (2.2.16)-(2.2.23) преобра-зуется в задачу Коши (2.3.8)-2.3.13) (вывод уравнений (2.3.8)-(2.3.13) с помощью инвариантного погружения приведен в приложении). Теорема 1 доказана.
ПИ-наблюдатель переменных состояния нелинейного
объекта с произвольными шумами. Рассмотрим
теперь случай, когда функции распределения вероятности погрешностей измерений ![]() и вектора погрешностей аппроксимации
и вектора погрешностей аппроксимации ![]() неизвестны. Если при этом известны
ковариационные функции этих погрешностей, то синтез ПИ‑наблюдателя переменных
состояния объекта управления (2.2.1) можно выполнять минимизацией функции
стоимости (2.2.9), матрицы весовых коэффициентов
неизвестны. Если при этом известны
ковариационные функции этих погрешностей, то синтез ПИ‑наблюдателя переменных
состояния объекта управления (2.2.1) можно выполнять минимизацией функции
стоимости (2.2.9), матрицы весовых коэффициентов ![]() и
и ![]() которой вычисляют по формулам (2.1.8) и (2.1.24).
которой вычисляют по формулам (2.1.8) и (2.1.24).
Если вновь ввести переменную ![]() по формуле (2.3.15), то
при минимизации функции стоимости (2.2.9) нужно решать ту же вариационную
задачу, что и при доказательстве теоремы 1. Поэтому уравнения (2.3.8)-(2.3.13) определяют оптимальный по критерию (2.2.9) ПИ‑наблюдатель переменных состояния объекта
управления (2.1.1), (2.1.2) с возмущающими воздействиями (2.1.10)-(2.1.13).
по формуле (2.3.15), то
при минимизации функции стоимости (2.2.9) нужно решать ту же вариационную
задачу, что и при доказательстве теоремы 1. Поэтому уравнения (2.3.8)-(2.3.13) определяют оптимальный по критерию (2.2.9) ПИ‑наблюдатель переменных состояния объекта
управления (2.1.1), (2.1.2) с возмущающими воздействиями (2.1.10)-(2.1.13).
Если ковариационные функции погрешностей аппроксимации
![]() неизвестны, то в уравнениях ПИ-наблюдателя
переменных состояния (2.3.8)-(2.3.13) можно использовать
любые положительно определенные матрицы
весовых коэффициентов
неизвестны, то в уравнениях ПИ-наблюдателя
переменных состояния (2.3.8)-(2.3.13) можно использовать
любые положительно определенные матрицы
весовых коэффициентов ![]() и
и ![]() , которые
можно рассматривать в качестве оценок матриц интенсивностей этих погрешностей.
, которые
можно рассматривать в качестве оценок матриц интенсивностей этих погрешностей.
Анализ алгоритма ПИ-наблюдателя. Из формул (2.3.8)-(2.3.13) видно, что алгоритм ПИ-наблюдателя переменных состояния по структуре подобен нелинейному фильтру Калмана, составленному для некоторой расширенной системы. ПИ-наблюдатель (2.3.8)-(2.3.13), как и фильтр Калмана, реализует алгоритм "прогноз - коррекция".
ПИ-наблюдатель (2.3.8)-(2.3.13), в отличие от фильтра
Калмана, формирует оценки переменных состояния объекта управления ![]() , апостериорные оценки возмущающих
воздействий
, апостериорные оценки возмущающих
воздействий ![]() и оценки
и оценки ![]() средних
значений погрешностей оценивания выходных сигналов измерительных устройств,
усредненные в скользящем временном окне. Поэтому ПИ-наблюдатель (2.3.8)-(2.3.13), в отличие от фильтра Калмана, обеспечивает несмещенные оценки
переменных состояния объекта управления даже в тех случаях, когда возмущающие
воздействия и погрешности измерений содержат неизвестные постоянные
составляющие.
средних
значений погрешностей оценивания выходных сигналов измерительных устройств,
усредненные в скользящем временном окне. Поэтому ПИ-наблюдатель (2.3.8)-(2.3.13), в отличие от фильтра Калмана, обеспечивает несмещенные оценки
переменных состояния объекта управления даже в тех случаях, когда возмущающие
воздействия и погрешности измерений содержат неизвестные постоянные
составляющие.
2.3.2. ПИД-наблюдатели переменных состояния
нелинейных объектов
ПИД-наблюдатель переменных состояния нелинейных объектов, оптимальный по критерию МАВ. Оптимальный по критерию МАВ наблюдатель переменных состояния нелинейного объекта управления (2.1.1)-(2.1.3) с гауссовскими цветными шумами определяет следующая теорема.
Теорема 2. Пусть
управляемый и наблюдаемый объект управления имеет нелинейное уравнение
состояния (2.3.1) с начальными условиями (2.3.2) и на этот объект действуют
возмущающие воздействия, изменение во времени которых описывают с помощью
В-сплайнов уравнениями (2.3.3), (2.3.4)
с начальными условиями (2.3.5). Пусть вектор выходных сигналов ![]() измерительных устройств и вектор переменных
состояния
измерительных устройств и вектор переменных
состояния ![]() связаны нелинейным уравнением (2.3.7),
где
связаны нелинейным уравнением (2.3.7),
где ![]() - вектор
средних значений погрешностей измерений;
- вектор
средних значений погрешностей измерений;![]() - вектор случайных состав-ляющих погрешностей измерений,
которые являются гауссовскими цветными шумами с нулевыми средними значениями и корреляционными
функциями (2.1.22). Пусть
начальные значения
- вектор случайных состав-ляющих погрешностей измерений,
которые являются гауссовскими цветными шумами с нулевыми средними значениями и корреляционными
функциями (2.1.22). Пусть
начальные значения ![]() и
и ![]() являются
гауссовскими случайными величинами, а погрешности аппроксимации
являются
гауссовскими случайными величинами, а погрешности аппроксимации ![]() -
гауссовские цветные шумы с нулевыми средними значениями и корреляционными
функциями (2.1.5).
-
гауссовские цветные шумы с нулевыми средними значениями и корреляционными
функциями (2.1.5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.