Тогда оценку ![]() переменных
состояния
переменных
состояния ![]() , оптимальную по критерию максимума
апостериорной вероятности (2.2.8),
формирует следующая динамическая система (ПИД-наблюдатель переменных
состояния):
, оптимальную по критерию максимума
апостериорной вероятности (2.2.8),
формирует следующая динамическая система (ПИД-наблюдатель переменных
состояния):
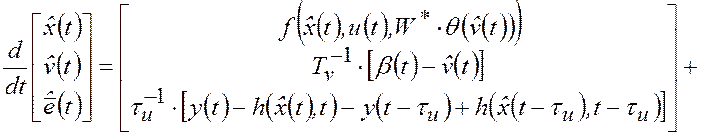
|
|
(2.3.24) |
|
|
(2.3.25) |
|
|
(2.3.26) |
с начальными условиями (2.3.11), где
|
|
(2.3.27) |
а матрицы ![]() ,
, ![]() и
и ![]() вычисляют
по формулам (2.3.12), (2.3.13) и (2.1.24).
вычисляют
по формулам (2.3.12), (2.3.13) и (2.1.24).
Для доказательства теоремы 2 вновь введем переменную ![]() по формулам (2.2.10) и заменим задачу
максимизации условной плотности (2.2.8) на эквивалентную задачу минимизации
функции стоимости (2.2.11) при ограничениях (2.2.1), (2.1.24)-(2.1.27). Дальнейшее доказательство теоремы 2 осуществляется так
же, как и доказательство теоремы 1.
по формулам (2.2.10) и заменим задачу
максимизации условной плотности (2.2.8) на эквивалентную задачу минимизации
функции стоимости (2.2.11) при ограничениях (2.2.1), (2.1.24)-(2.1.27). Дальнейшее доказательство теоремы 2 осуществляется так
же, как и доказательство теоремы 1.
ПИД-наблюдатель переменных состояния нелинейного
объекта с произвольными шумами. Рассмотрим
теперь случай, когда функции распределения вероятности погрешностей измерений ![]() и вектора погрешностей аппроксимации
и вектора погрешностей аппроксимации ![]() неизвестны.
неизвестны.
Синтез ПИД‑наблюдателя переменных состояния объекта управления (2.2.1) можно выполнять минимизацией функции стоимости (2.2.11) обобщенного МНК с ограничениями (2.2.1), (2.1.8) и (2.1.24)-(2.1.27). Очевидно, что эта вариационная задача совпадает с вариационной задачей, составленной по условиям теоремы 2. Поэтому ПИД‑наблюдатель (2.3.24)-(2.3.27), (2.3.12), (2.3.13), (2.1.24) формирует оценки переменных состояния нелинейного объекта (2.2.1) с произвольными шумами, оптимальные по критерию (2.2.11) обобщенного МНК.
Пример 1. Нелинейный объект имеет следующие уравнения состояния:
|
|
(2.3.28) |
|
|
(2.3.29) |
где ![]() - пространственная координата объекта в системе координат, в центре
которой находится устройство, измеряющее расстояние до объекта:
- пространственная координата объекта в системе координат, в центре
которой находится устройство, измеряющее расстояние до объекта:
|
|
(2.3.30) |
![]() ,
, ![]() - скорость движения
объекта и управляющее воздействие, недоступные прямым измерениям;
- скорость движения
объекта и управляющее воздействие, недоступные прямым измерениям; ![]() - возмущающее воздей-ствие,
которое является неизвестной функцией пространственной координаты объекта;
- возмущающее воздей-ствие,
которое является неизвестной функцией пространственной координаты объекта; ![]() - постоянная
времени объекта, значение которой известно приближенно;
- постоянная
времени объекта, значение которой известно приближенно; ![]() - случайная погрешность измерений с дисперсией
- случайная погрешность измерений с дисперсией ![]() .
.
Объект (2.3.28)-(2.3.30), имеющий
постоянную времени ![]() (известное наблюдателю значение
постоянной времени
(известное наблюдателю значение
постоянной времени ![]() ), движется под действием
управляющего и возмущающего воздействий, законы изменения которых от своих
аргументов приведены на рисунках 2.5 и 2.6.
), движется под действием
управляющего и возмущающего воздействий, законы изменения которых от своих
аргументов приведены на рисунках 2.5 и 2.6.
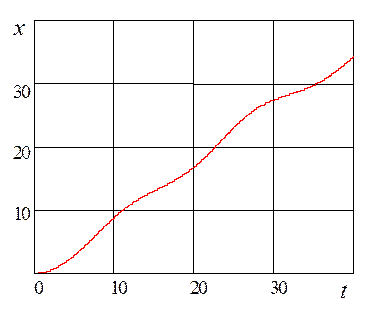
На рисунке 2.7 изображен график изменения скорости движения объекта. На рисунке 2.8 приведены результаты измерений текущих значений пространственной координаты этого объекта.
|
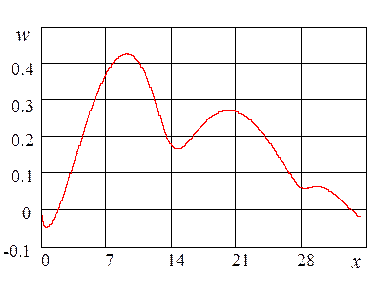
Рис. 2.5. Изменение возмущающего воздействия вдоль пространственной координаты |
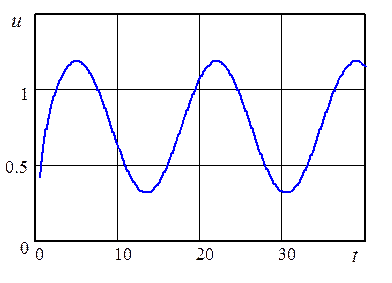
Рис. 2.6. Изменение управляющего воздействия во времени |
Результаты измерений текущих значений пространственной
координаты, выполненные с относительной погрешностью ![]() ,
использовались для оценивания текущих значений скорости движения объекта
(одновременно с идентификацией его постоянной времени) с помощью рекуррентного
метода наименьших квадратов (фильтра Калмана) и алгоритма (2.3.8)-(2.3.13) при величине временного
окна
,
использовались для оценивания текущих значений скорости движения объекта
(одновременно с идентификацией его постоянной времени) с помощью рекуррентного
метода наименьших квадратов (фильтра Калмана) и алгоритма (2.3.8)-(2.3.13) при величине временного
окна ![]() и
и ![]() .
.
|
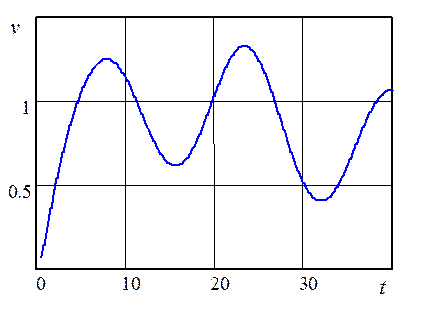
Рис. 2.7. Изменение скорости движения объекта во времени |
Рис. 2.8. Изменение во времени выходного сигнала измерительного устройства |
Результаты оценивания скорости движения объекта с помощью указанных методов приведены на рисунке 2.9.
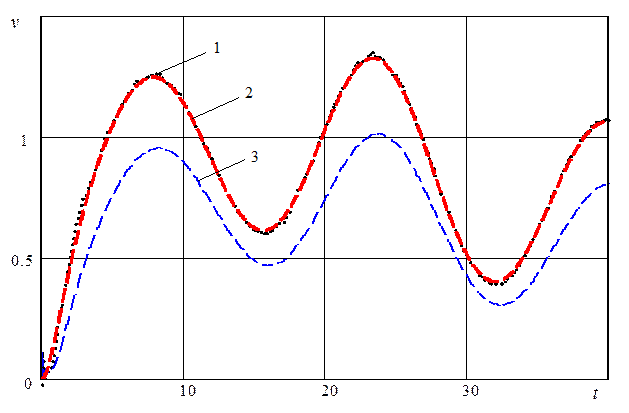
Рис. 2.9. Результаты оценивания скорости движения объекта
На рисунке 2.9 изображены изменение во времени действи-тельной
скорости движения объекта (линия 2), оценка скорости, вычисленная с помощью
разработанного алгоритма (линия 1), и оценка скорости по алгоритму
фильтра Калмана (линия 3). Резуль-таты моделирования (рис. 2.9)
показывают, что в этом примере алгоритм (2.3.8)-(2.3.13) обеспечивает несмещенные оценки скорости движения
объекта со среднеквадратическим отклонением погреш-ности оценивания ![]() . В то же время оценки фильтра Калмана (линия
2 на рис. 2.9) имеют существенное смещение.
. В то же время оценки фильтра Калмана (линия
2 на рис. 2.9) имеют существенное смещение.
2.4. ПИ-наблюдатель переменных состояния объекта
с неизвестной математической моделью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.